Abstract
A Budgeted Markov Decision Process (BMDP) is an extension of a Markov Decision Process to critical applications requiring safety constraints. It relies on a notion of risk implemented in the shape of a cost signal constrained to lie below an — adjustable — threshold. So far, BMDPs could only be solved in the case of finite state spaces with known dynamics. This work extends the state-of-the-art to continuous spaces environments and unknown dynamics. We show that the solution to a BMDP is a fixed point of a novel Budgeted Bellman Optimality operator. This observation allows us to introduce natural extensions of Deep Reinforcement Learning algorithms to address large-scale BMDPs. We validate our approach on two simulated applications: spoken dialogue and autonomous driving.
Paper and Bibtex
Citation
Carrara N., Leurent, E., Laroche R., Urvoy T., Maillard, O-A., and Pietquin O., 2019.
Budgeted Reinforcement Learning in Continuous State Space. In Advances in Neural Information Processing Systems.
[Bibtex]
@incollection{Carrara2019,
title = {Budgeted Reinforcement Learning in Continuous State Space},
author = {Carrara, Nicolas and Leurent, Edouard and Laroche, Romain
and Urvoy, Tanguy and Maillard, Odalric-Ambrym and Pietquin, Olivier},
booktitle = {Advances in Neural Information Processing Systems 32},
editor = {H. Wallach and H. Larochelle and A. Beygelzimer and
F. d\textquotesingle Alch\'{e}-Buc and E. Fox and R. Garnett},
pages = {9299--9309},
year = {2019},
publisher = {Curran Associates, Inc.},
url = {http://papers.nips.cc/paper/
9128-budgeted-reinforcement-learning-in-continuous-state-space.pdf}
}
Experiments
Optimal Budgeted Policies
Driving styles
We show samples of driving styles emerging from constraining the time spent on the opposite lane with different constraint budget values. The budget enables to control in real-time the tradeoff between efficiency and safety.
| Budget | Behaviours |
|---|---|
 |
|
 |
|
 |
Dialogue examples
In the following table, we display two dialogues done with the same BFTQ policy. The policy is given two budgets to respect in expectation, and
. For budget 0, one can see that the system never uses the
ask_num_pad action. Instead, it uses ask_oral, an action subject to recognition errors. The system keeps asking for the same slot 2, because it has the lowest speech recognition score. It eventually summarizes the form to the user, but then reaches the maximum dialogue length and thus faces a dialogue failure. For budget 0.5, the system first asks in a safe way, with ask_oral. It may want to ask_num_pad if one of the speech recognition score is low. Then, the system proceeds to a confirmation of the slot values. If it is incorrect, the system continues the dialogue using unsafe the ask_num_pad action to be certain of the slot values.
| turn | ||
|---|---|---|
| turn 0 | valid slots : [0, 0, 0] srs : [ None None None ] system says “ASK_ORAL(1)” user says “INFORM” |
valid slots : [0, 0, 0] srs : [ None None None ] system says “ASK_ORAL(2)” user says “INFORM” |
| turn 1 | valid slots : [0, 0, 0] srs : [ None 0.48 None ] system says “ASK_ORAL(2)” user says “INFORM” |
valid slots : [0, 0, 1] srs : [ None None 0.56 ] system says “ASK_ORAL(0)” user says “INFORM” |
| turn 2 | valid slots : [0, 0, 0] srs : [ None 0.48 0.22 ] system says “ASK_ORAL(0)” user says “INFORM” |
valid slots : [0, 0, 1] srs : [ 0.30 None 0.56 ] system says “ASK_ORAL(1)” user says “INFORM” |
| turn 3 | valid slots : [0, 0, 0] srs : [ 0.62 0.48 0.22 ] system says “ASK_ORAL(2)” user says “INFORM” |
valid slots : [0, 0, 1] srs : [ 0.30 0.54 0.56 ] system says “ASK_ORAL(0)” user says “INFORM” |
| turn 4 | valid slots : [0, 0, 0] srs : [ 0.62 0.48 0.66 ] system says “ASK_ORAL(1)” user says “INFORM” |
valid slots : [0, 0, 1] srs : [ 0.68 0.54 0.56 ] system says “ASK_NUM_PAD(1)” user says “INFORM” |
| turn 5 | valid slots : [0, 1, 0] srs : [ 0.62 0.56 0.66 ] system says “ASK_ORAL(2)” user says “INFORM” |
valid slots : [0, 1, 1] srs : [ 0.68 1.00 0.56 ] system says “SUMMARIZE_AND_INFORM” user says “DENY_SUMMARIZE” |
| turn 6 | valid slots : [0, 1, 0] srs : [ 0.62 0.56 0.14 ] system says “ASK_ORAL(2)” user says “INFORM” |
valid slots : [0, 1, 1] srs : [ 0.68 1.00 0.56 ] system says “ASK_NUM_PAD(2)” user says “INFORM” |
| turn 7 | valid slots : [0, 1, 1] srs : [ 0.62 0.56 0.30 ] system says “ASK_ORAL(2)” user says “INFORM” |
valid slots : [0, 1, 1] srs : [ 0.68 1.00 1.00 ] system says “SUMMARIZE_AND_INFORM” user says “DENY_SUMMARIZE” |
| turn 8 | valid slots : [0, 1, 1] srs : [ 0.62 0.56 0.49 ] system says “ASK_ORAL(2)” user says “INFORM” |
valid slots : [0, 1, 1] srs : [ 0.68 1.00 1.00 ] system says “ASK_NUM_PAD(0)” user hangs up ! |
| turn 9 | valid slots : [0, 1, 1] srs : [ 0.62 0.56 0.65 ] system says “SUMMARIZE_AND_INFORM” max size reached ! |
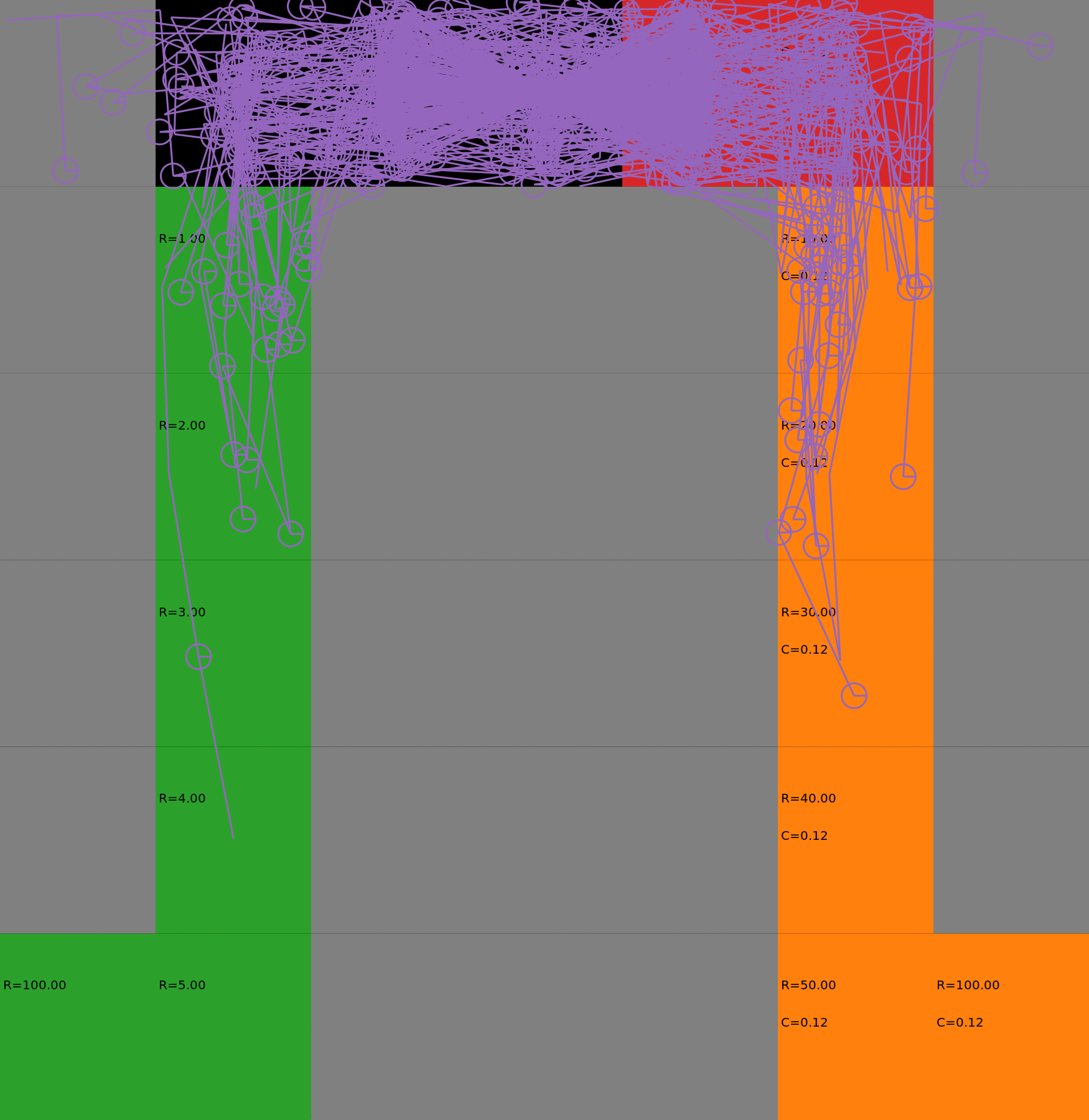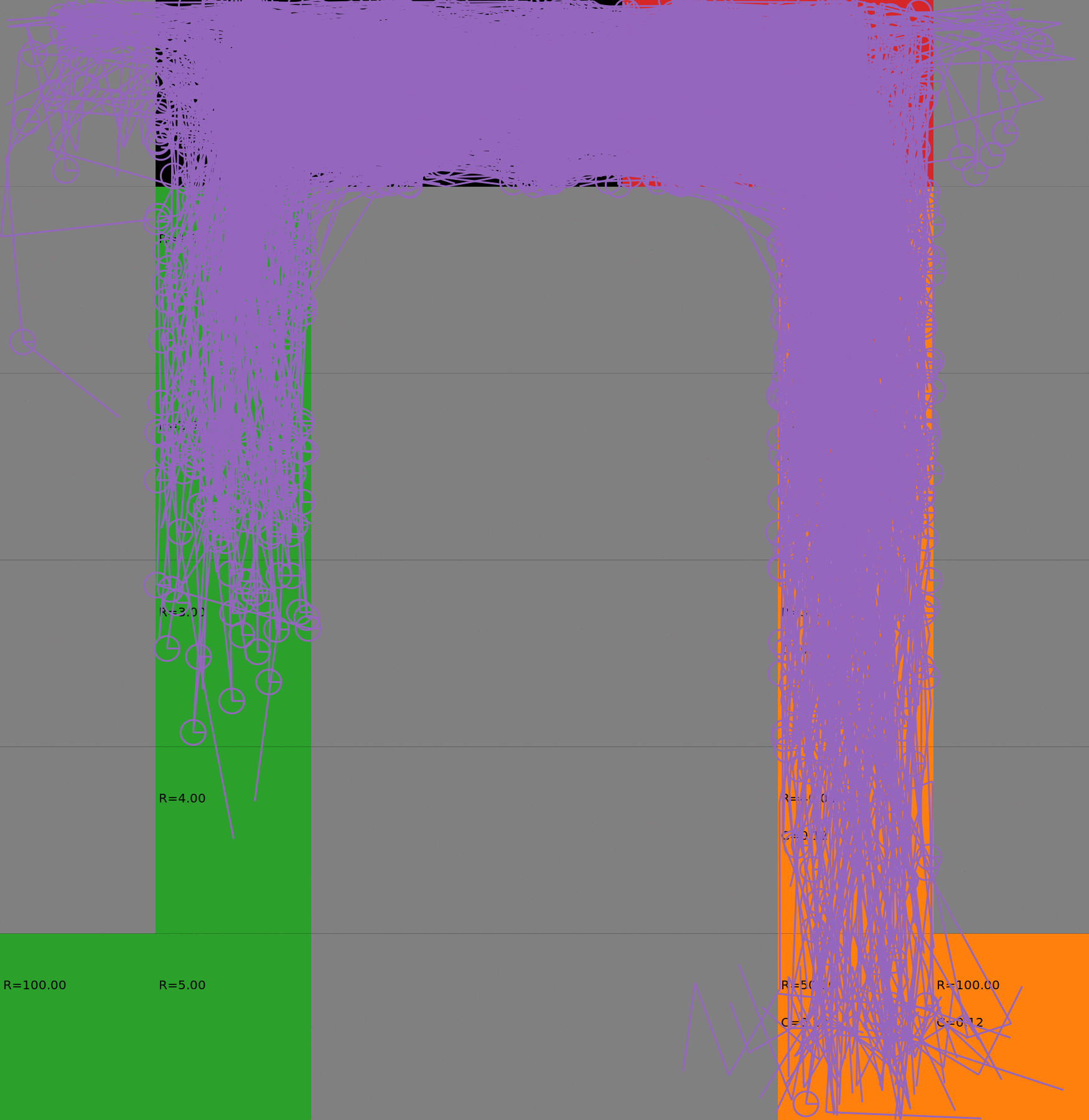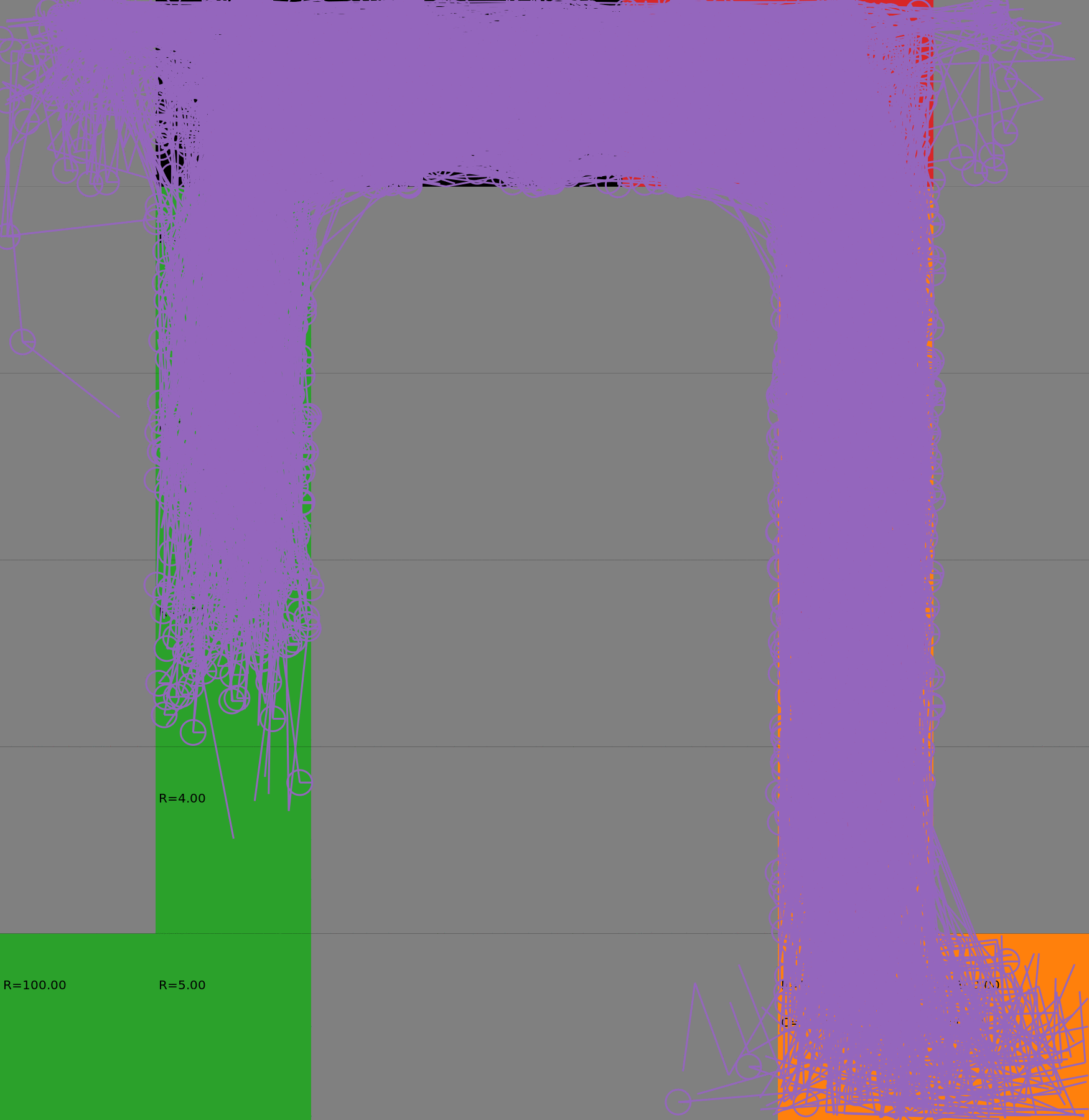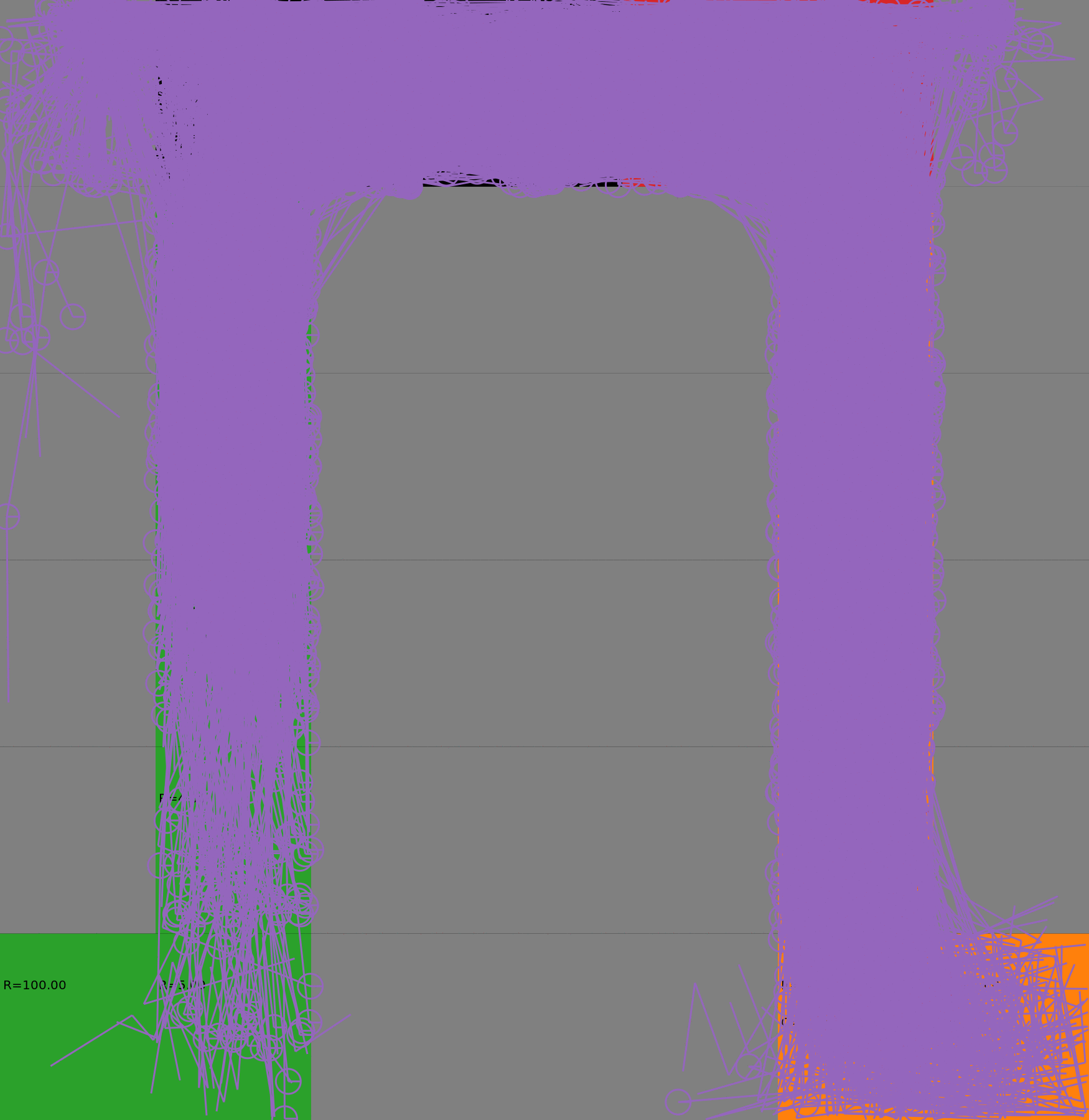
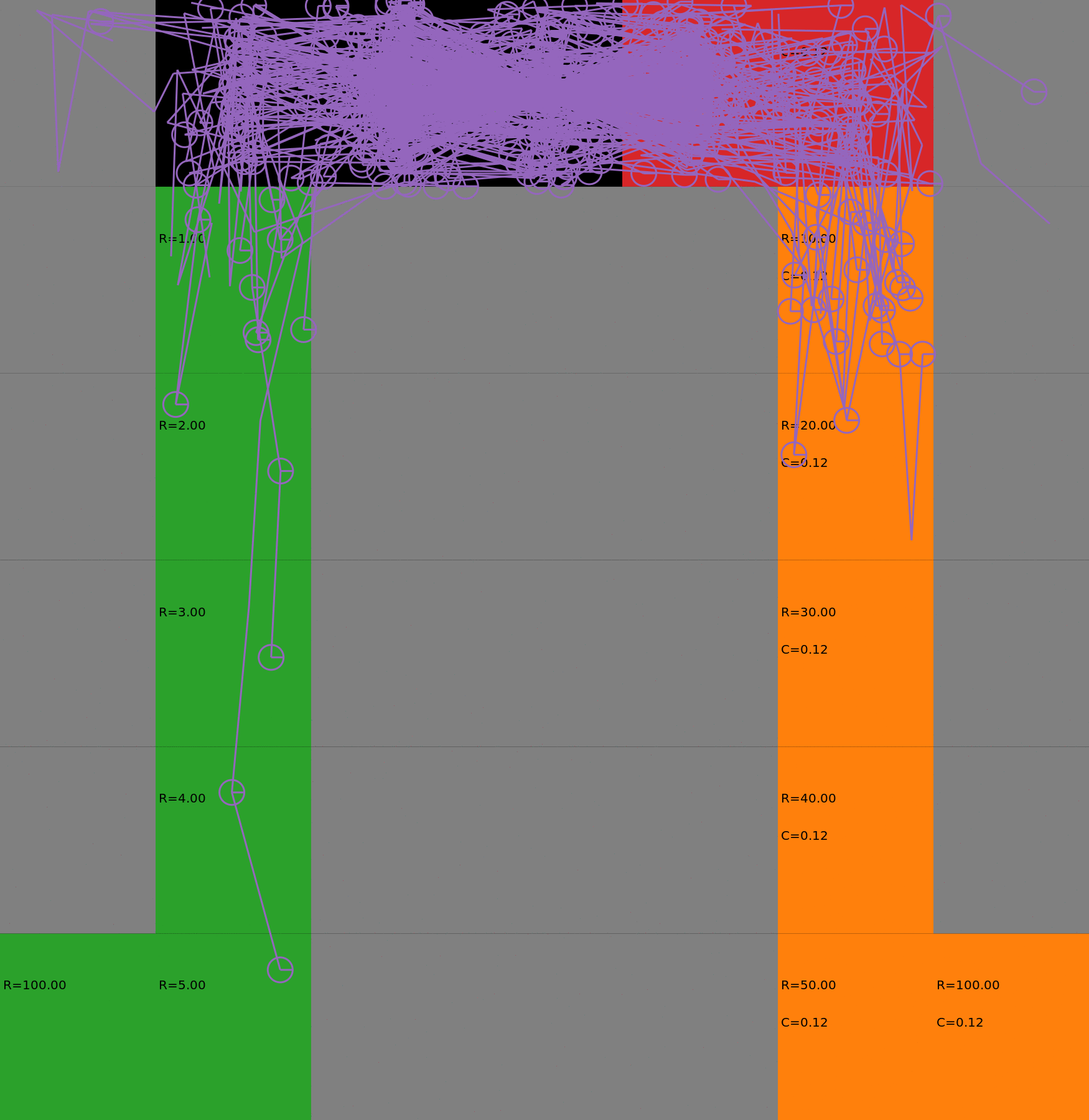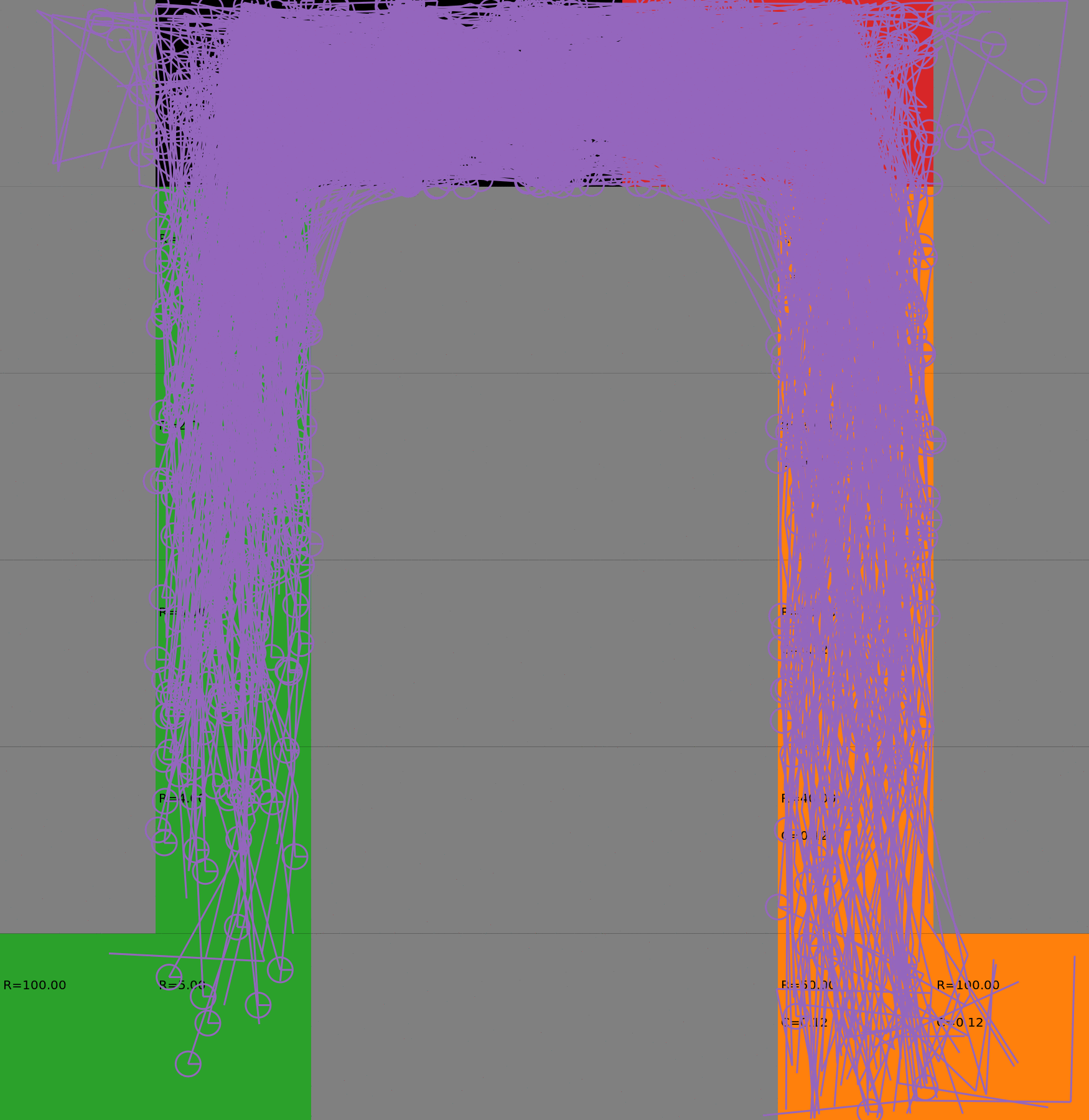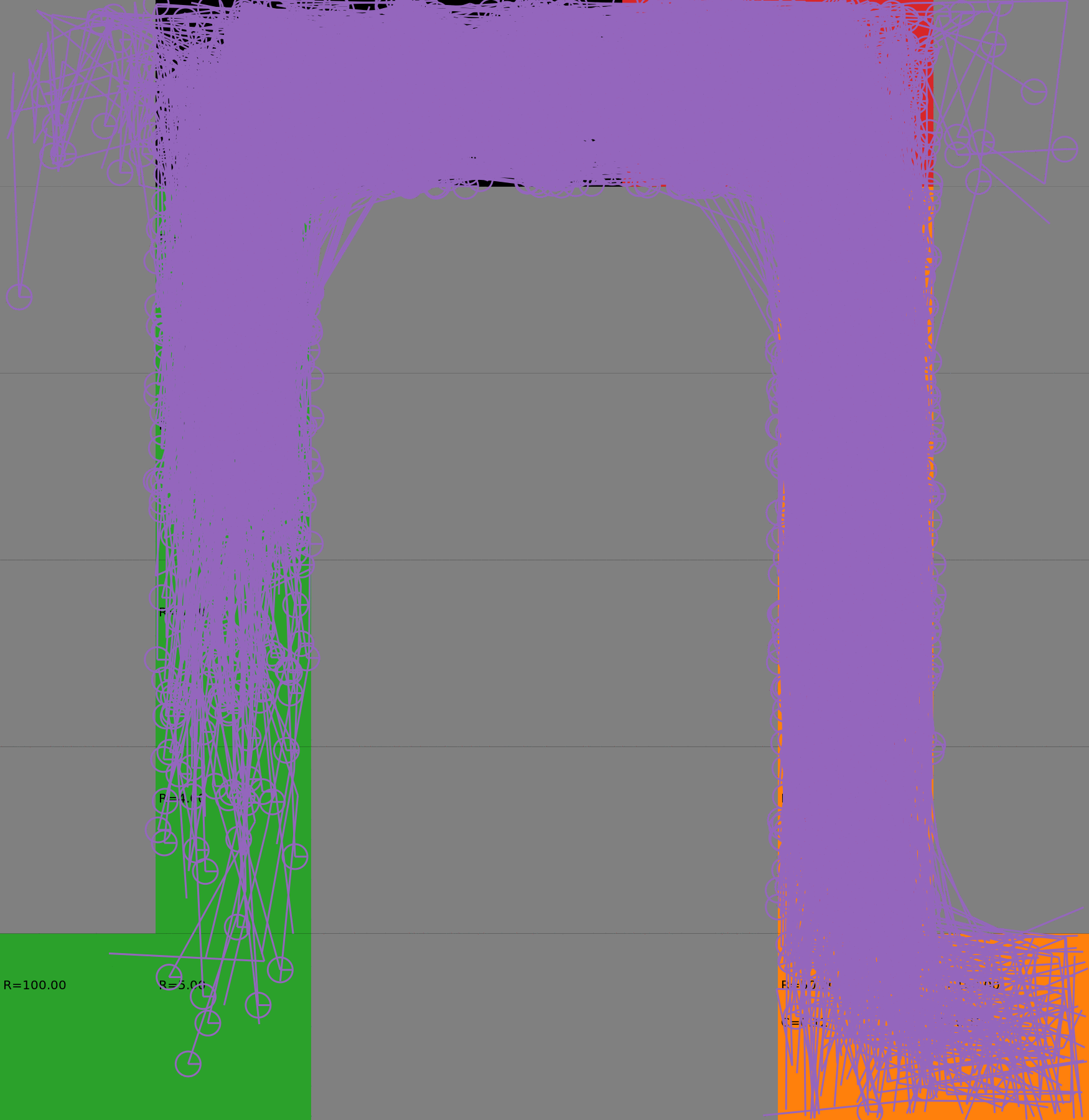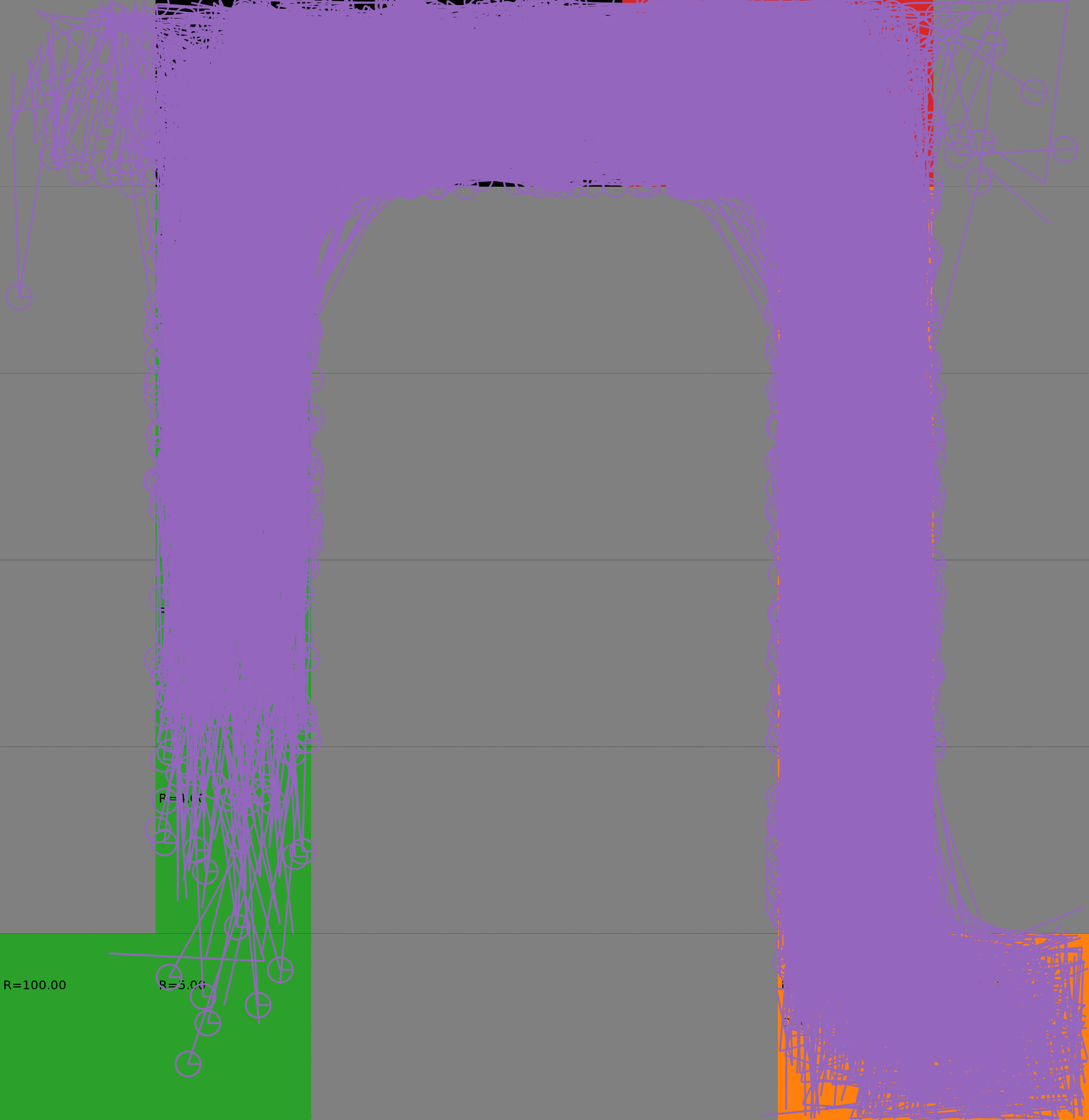
Risk-Sensitive Exploration
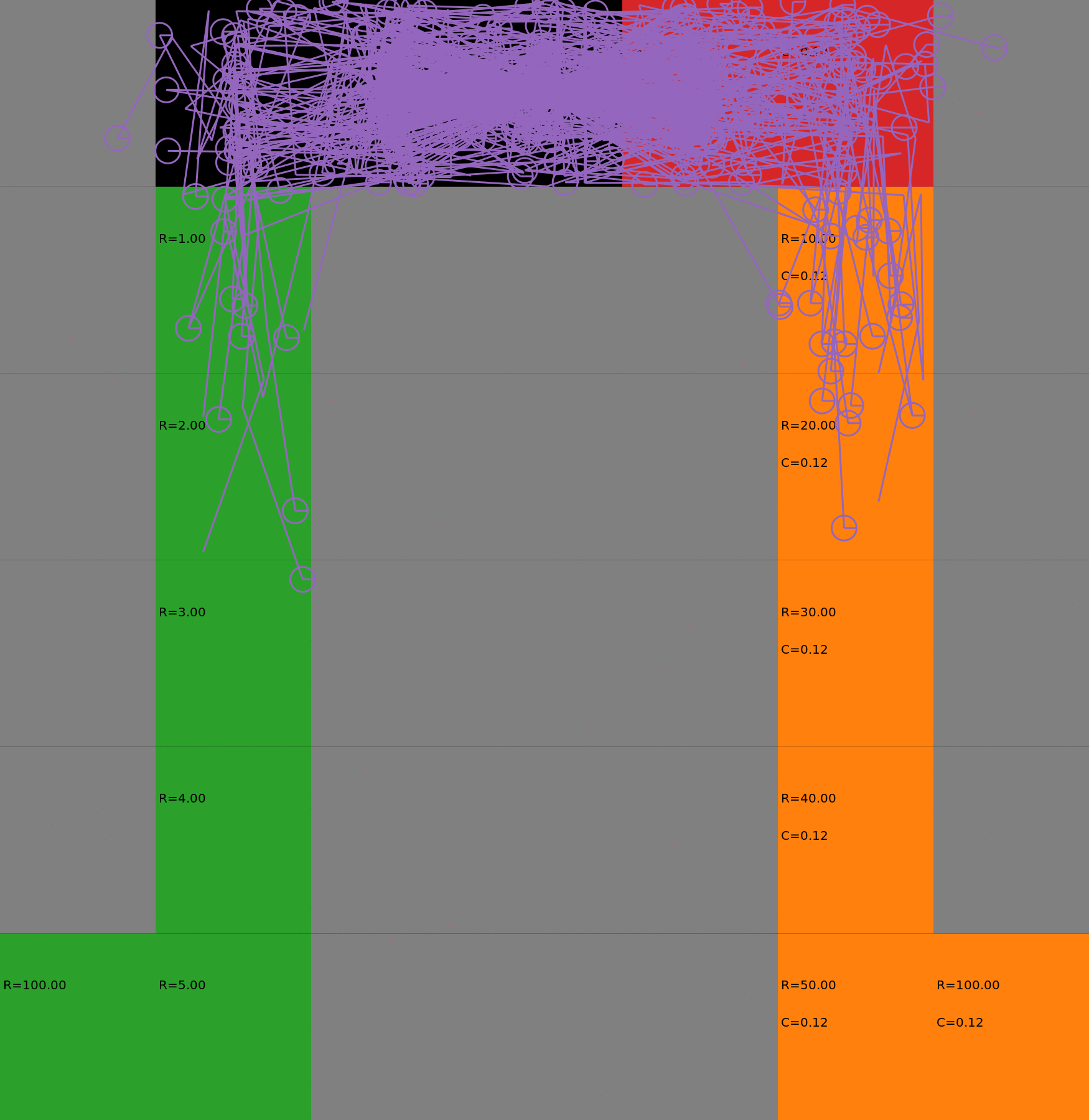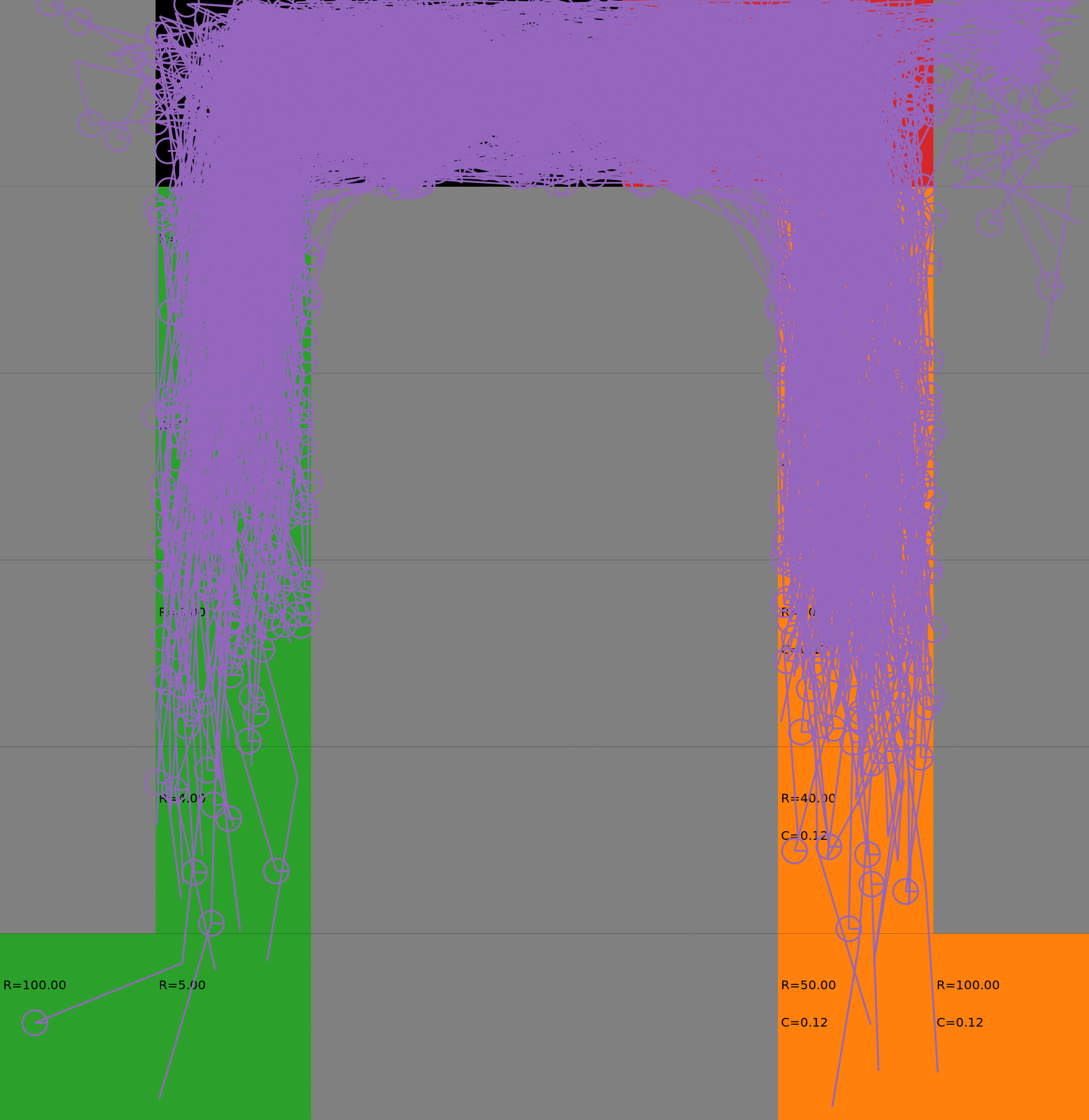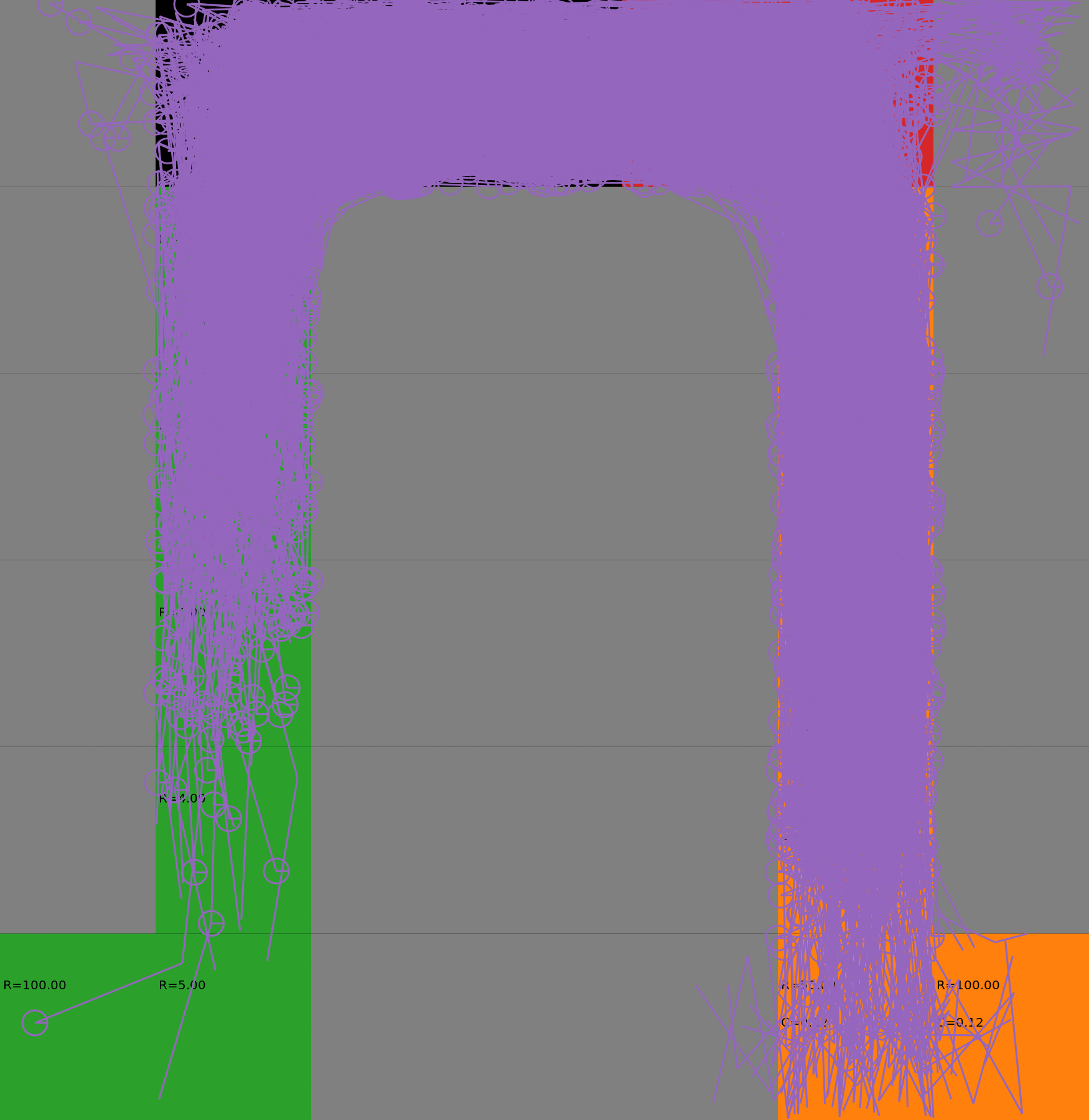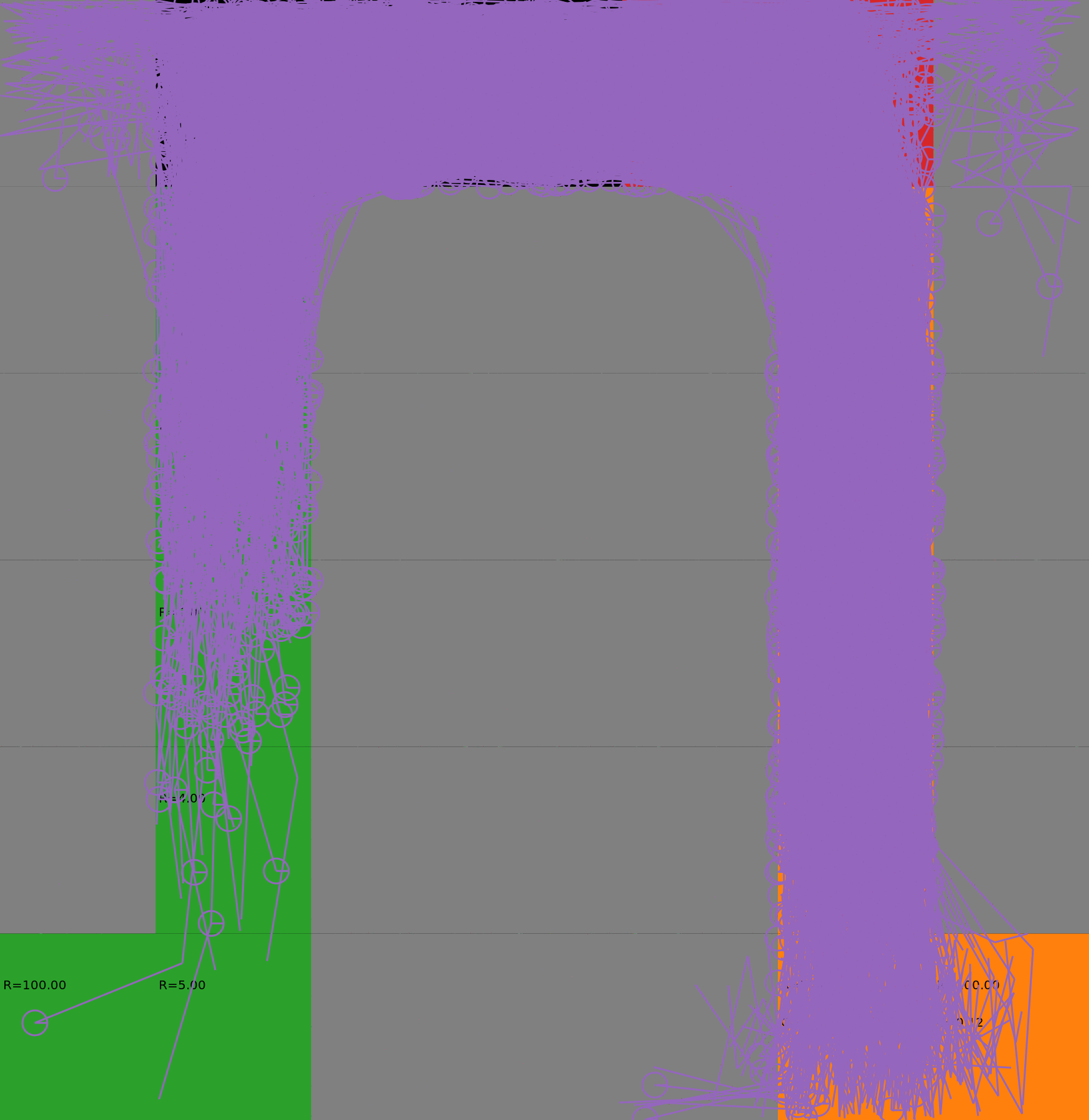
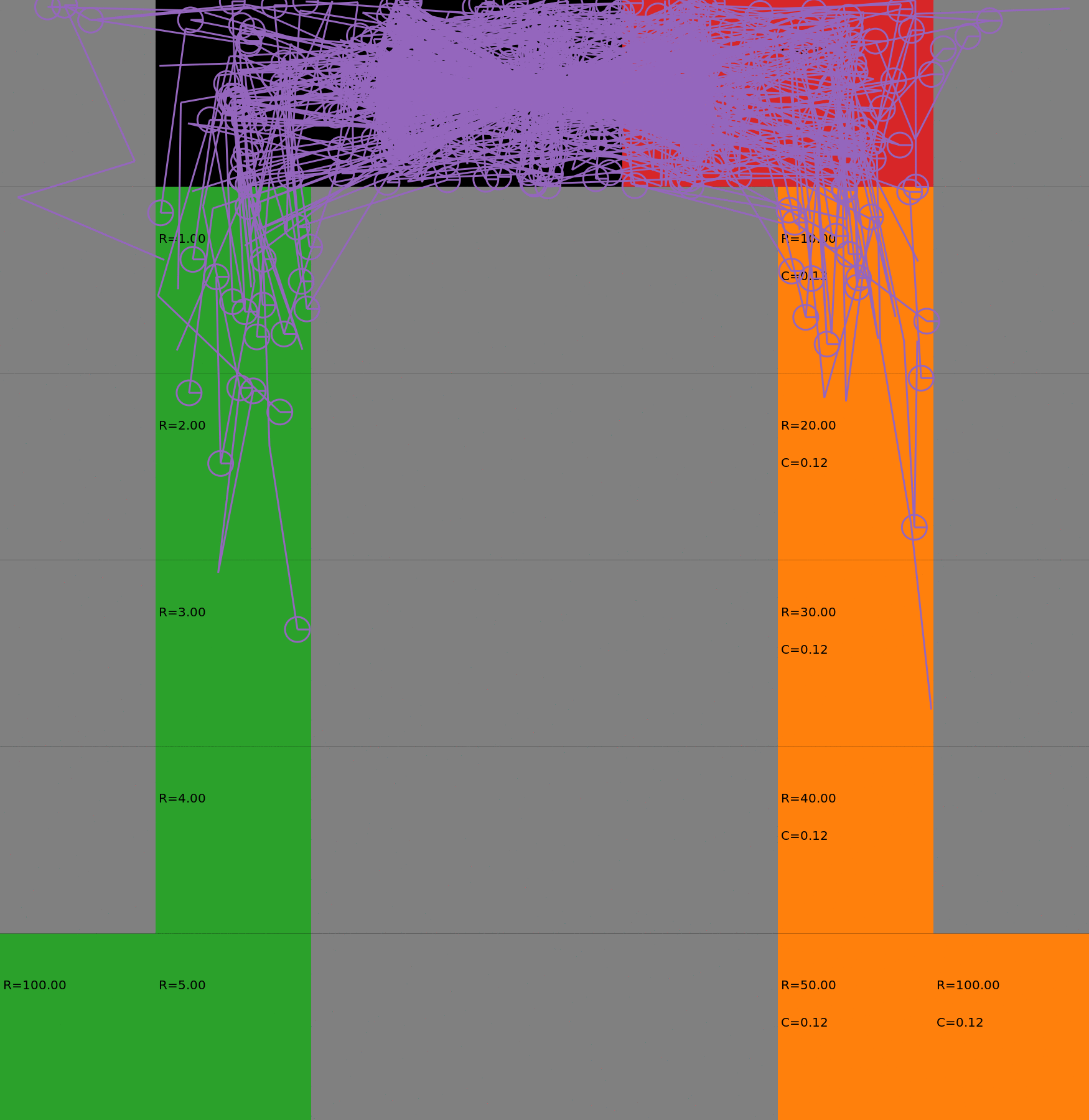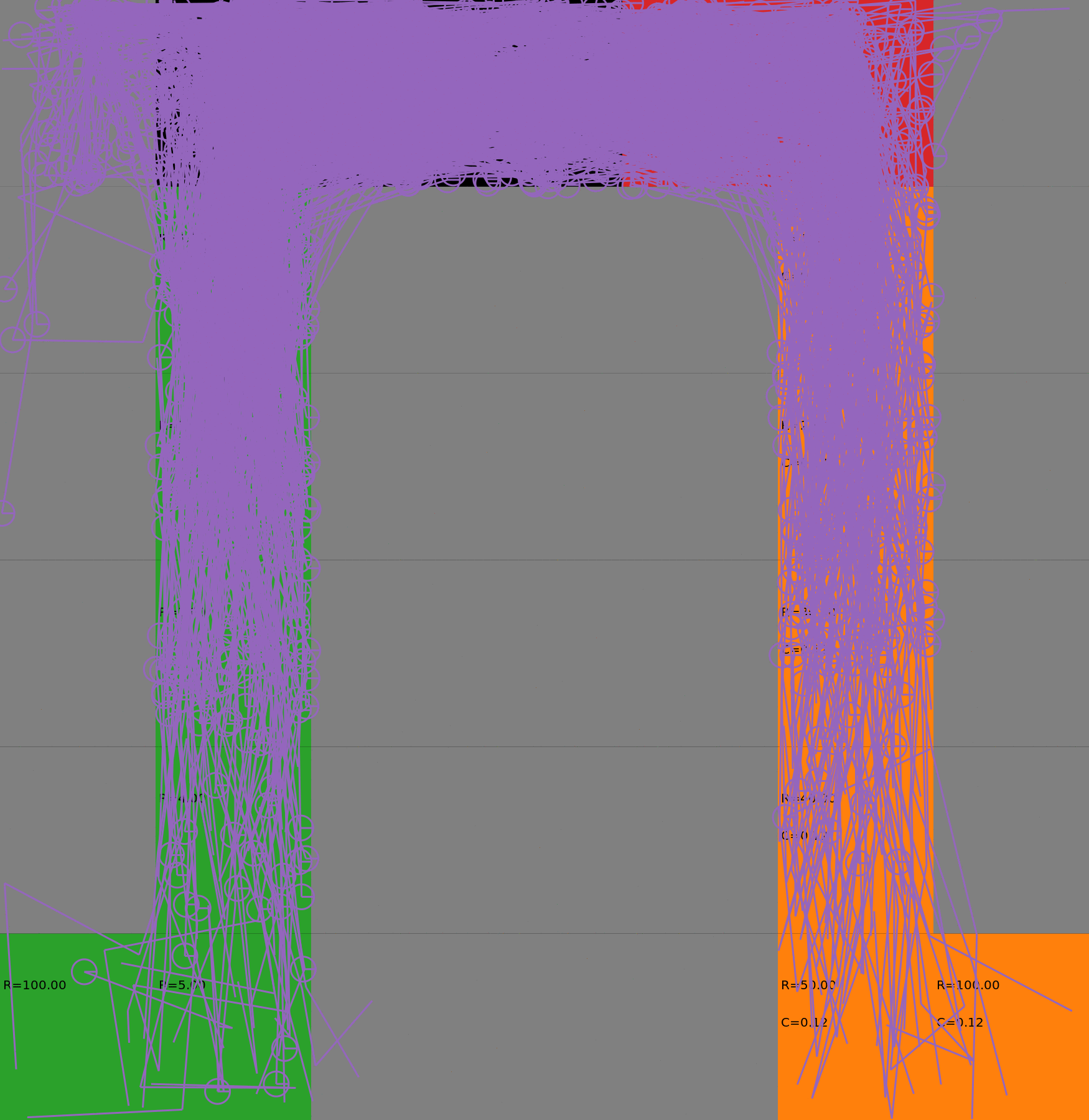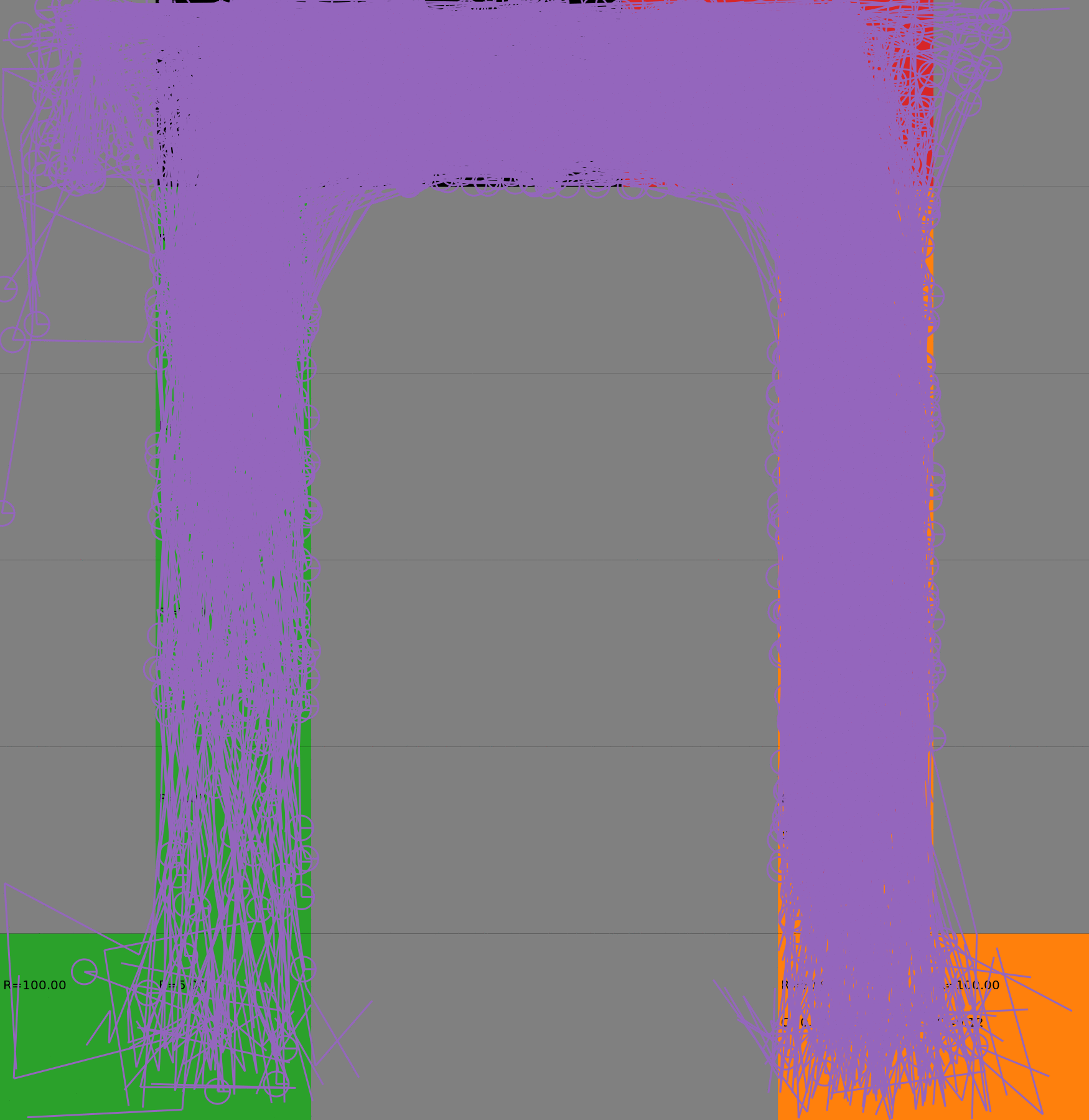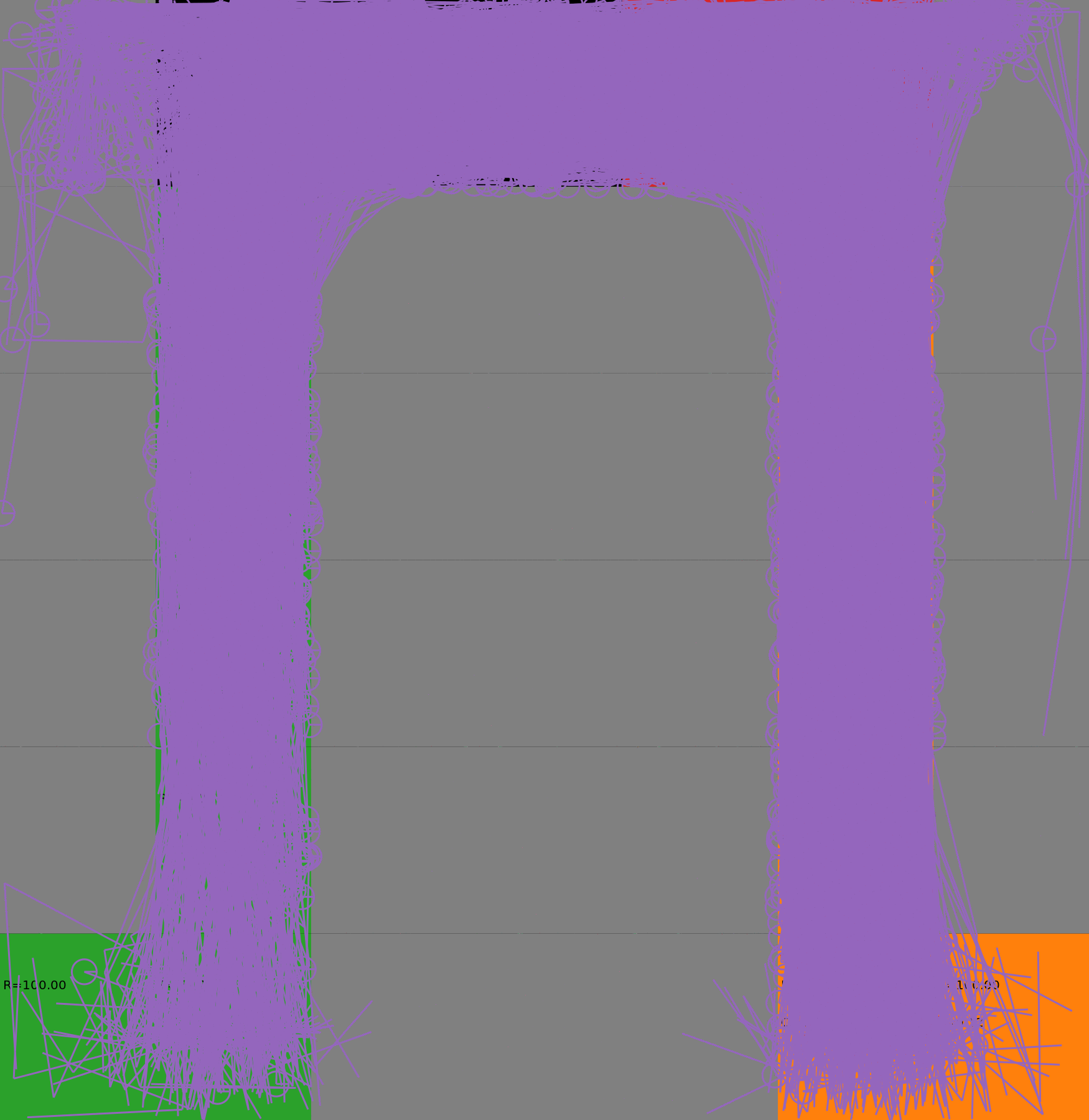
We compare two approaches for contructing a batch of samples. The animations display the trajectories collected in each intermediate subbatch. The first row corresponds to a classical risk neutral epsilon-greedy exploration policy while the second row showcases a risk-sensitive exploration strategy introduced in the paper. Each animation corresponds to a different seed.
Risk-neutral strategy
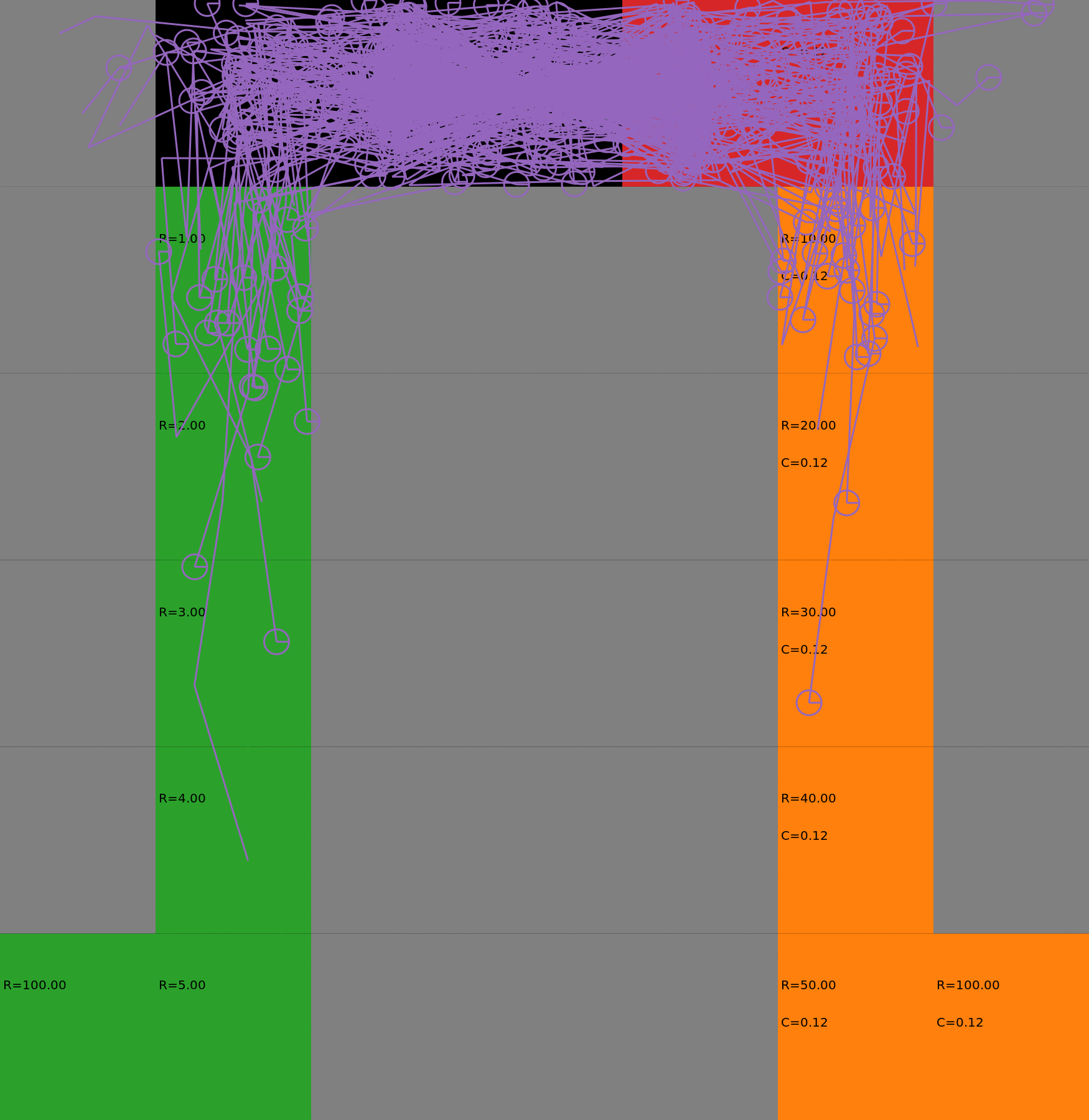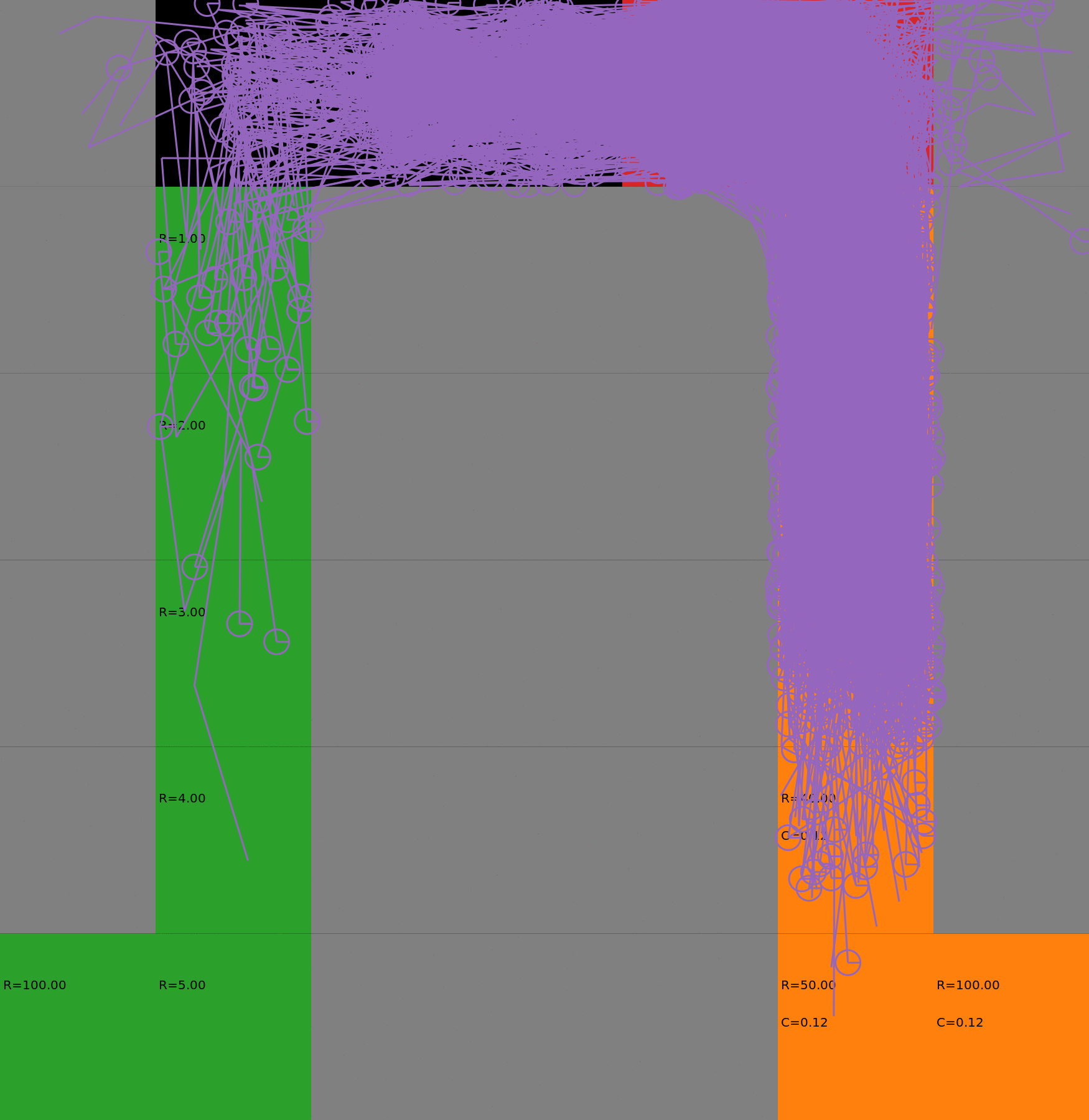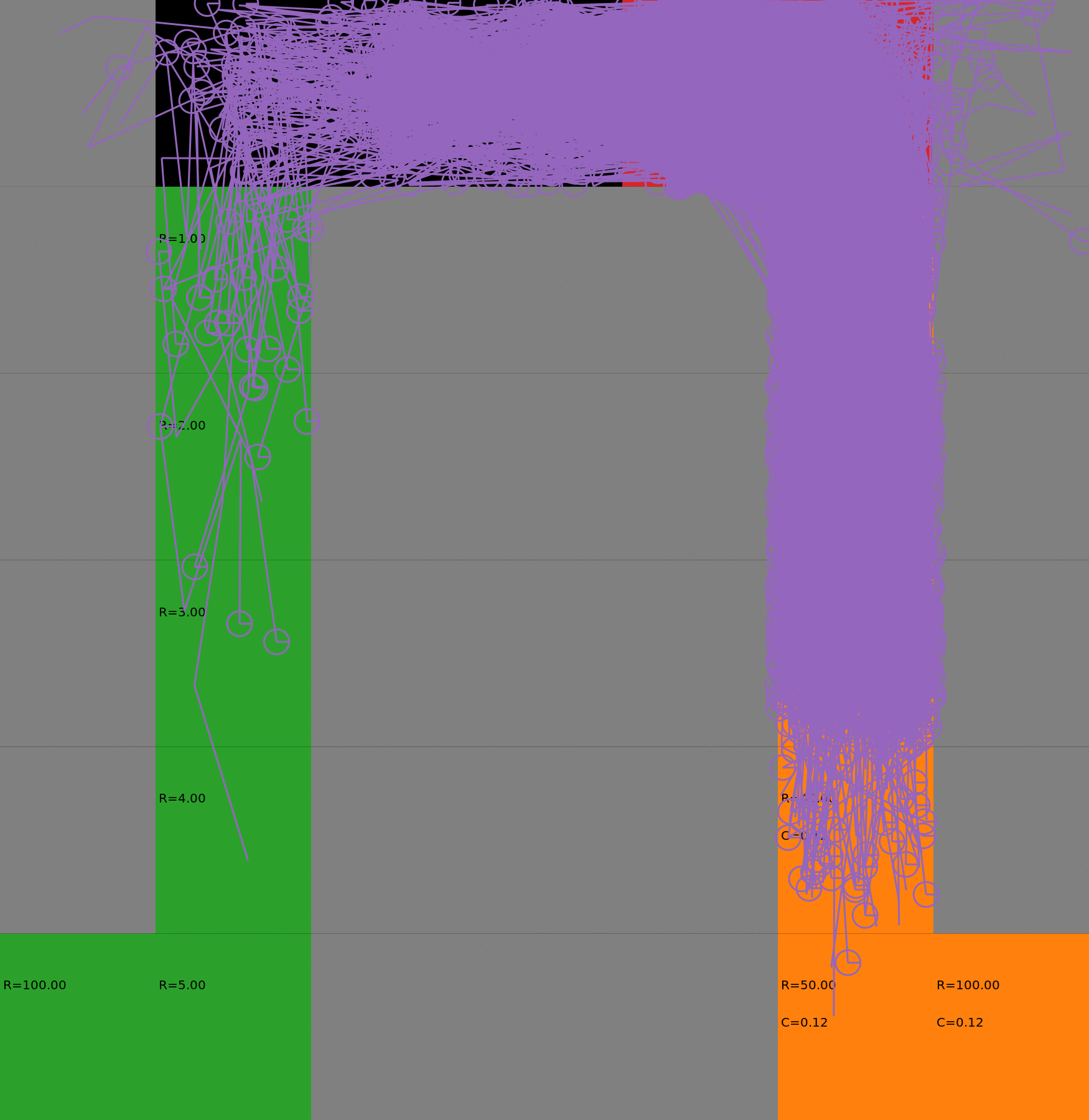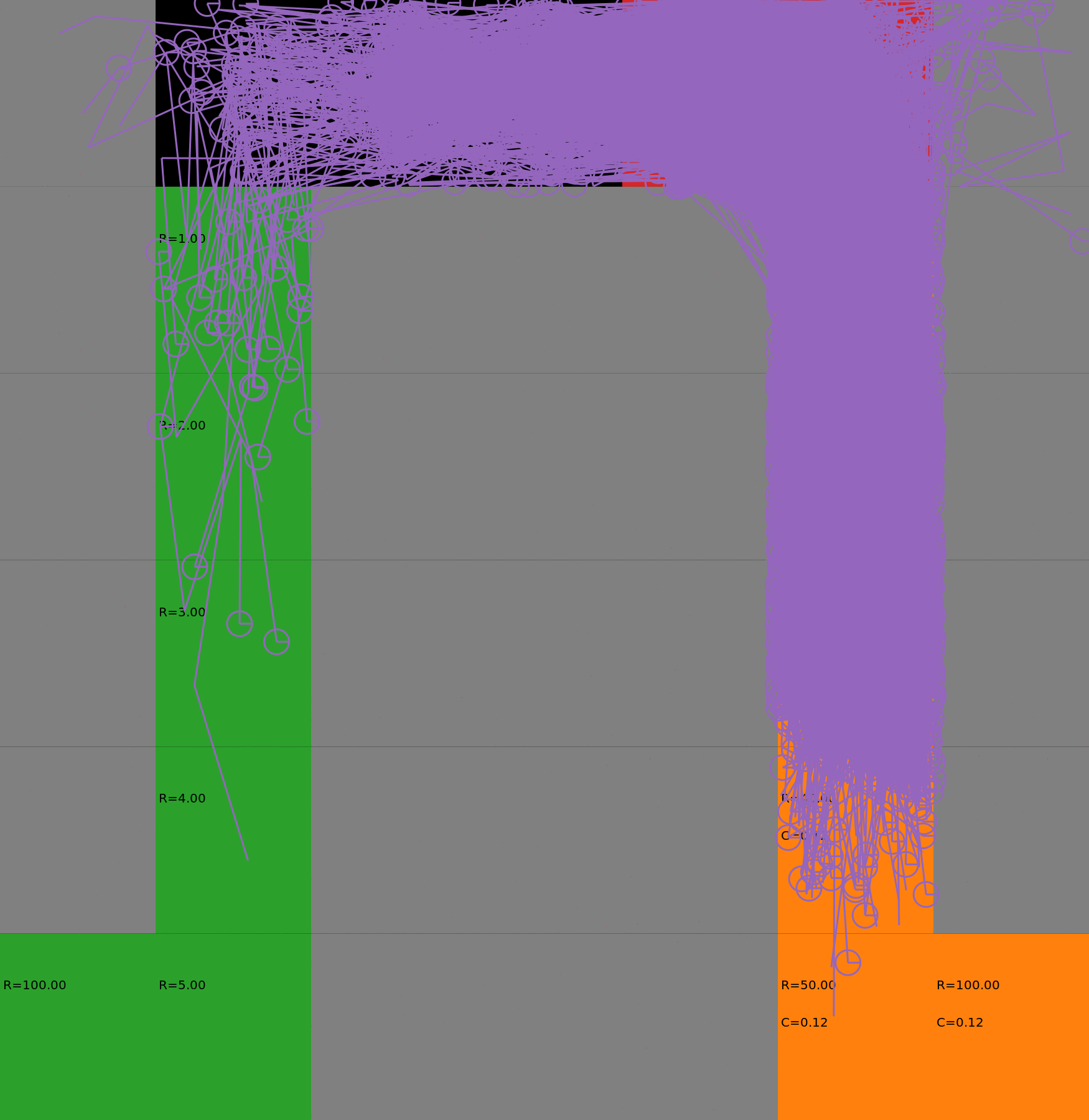
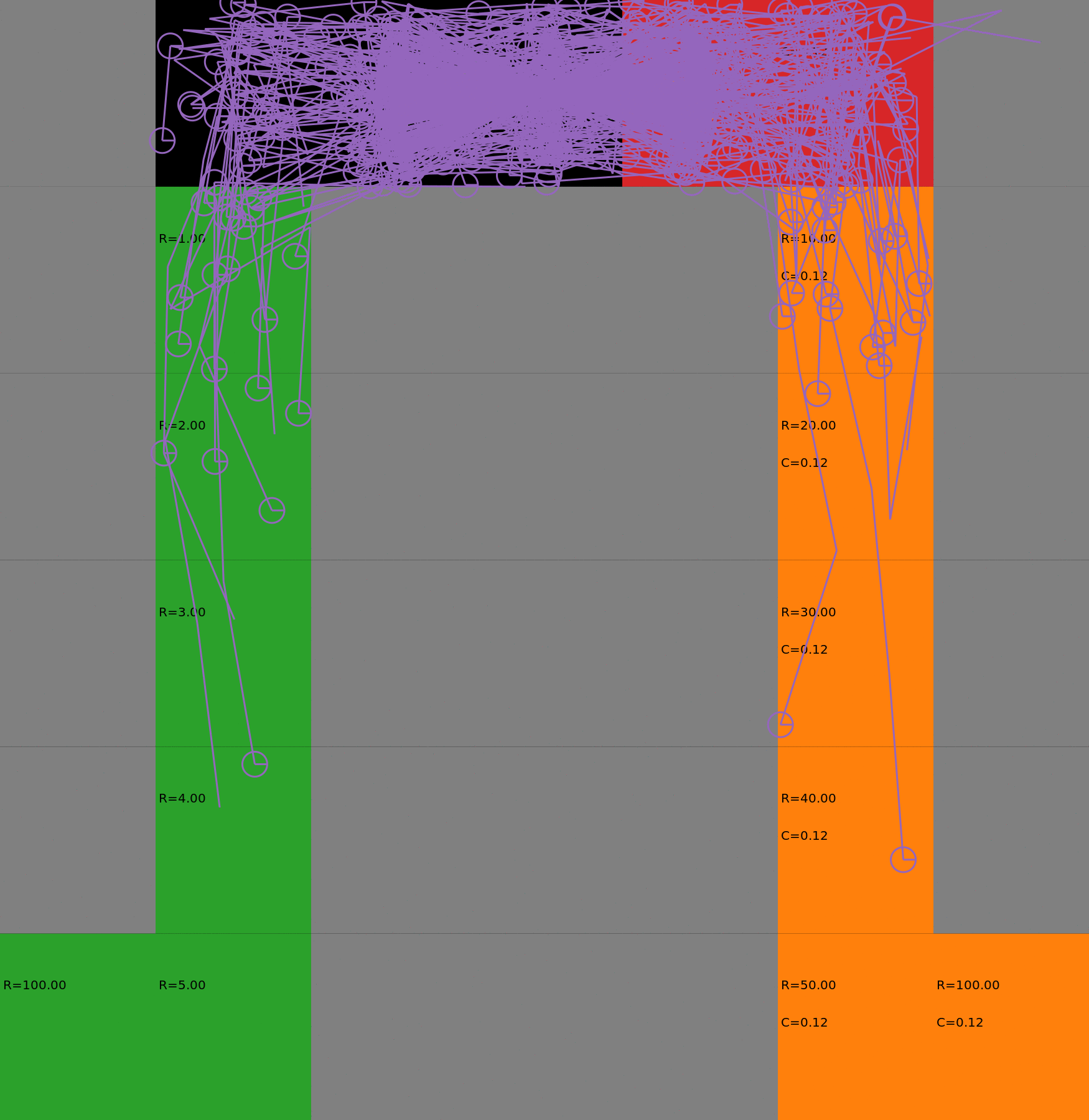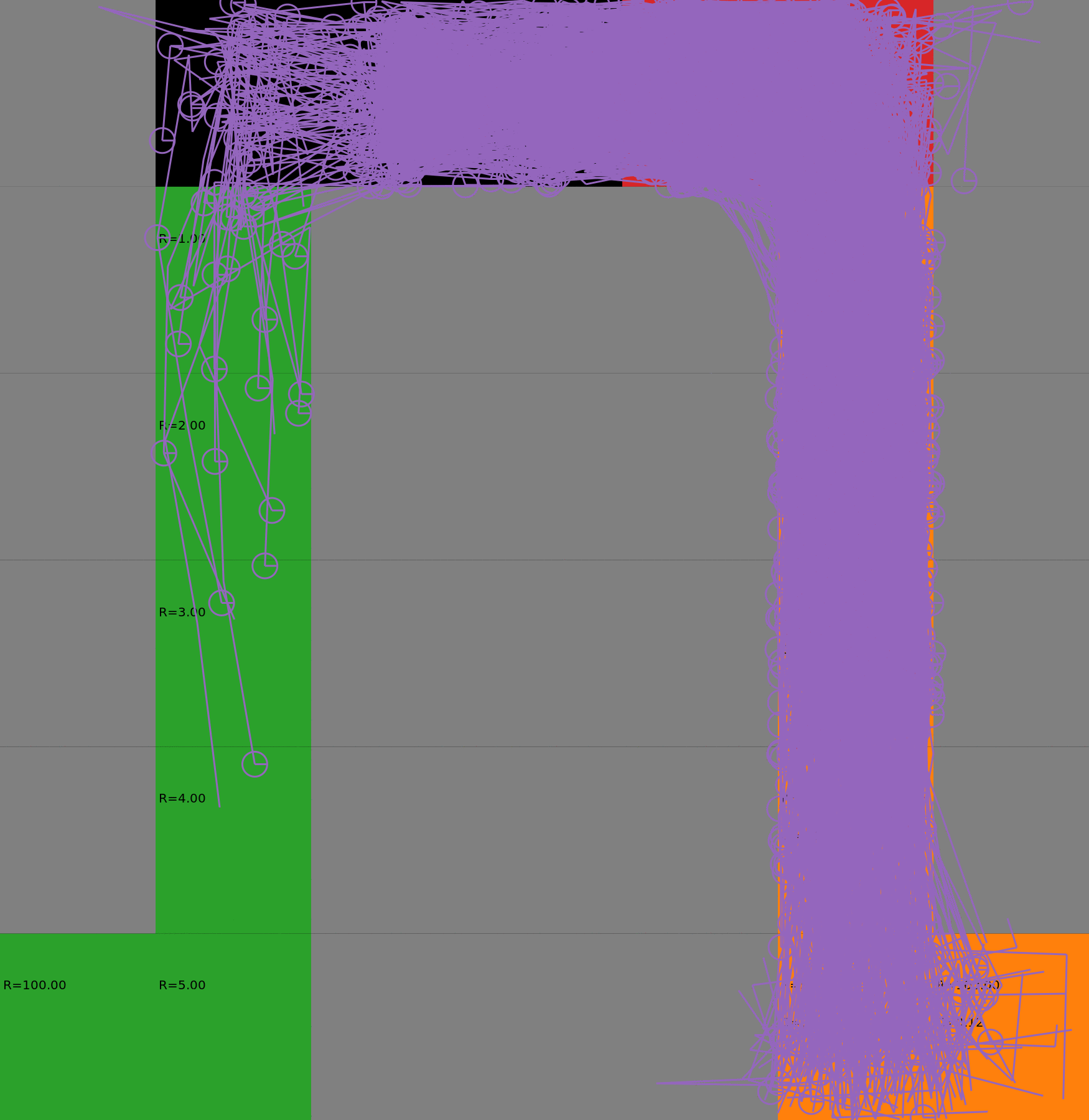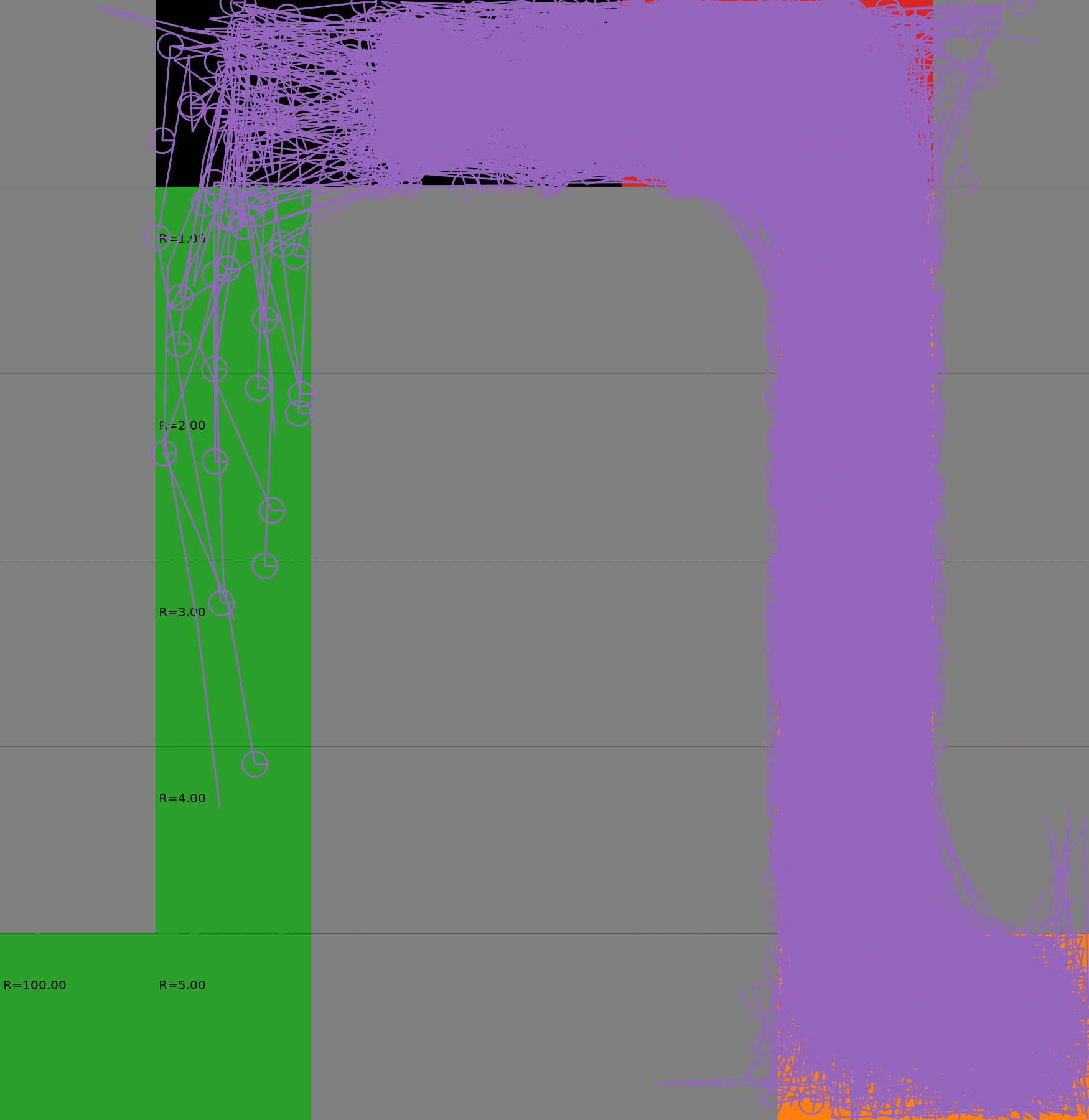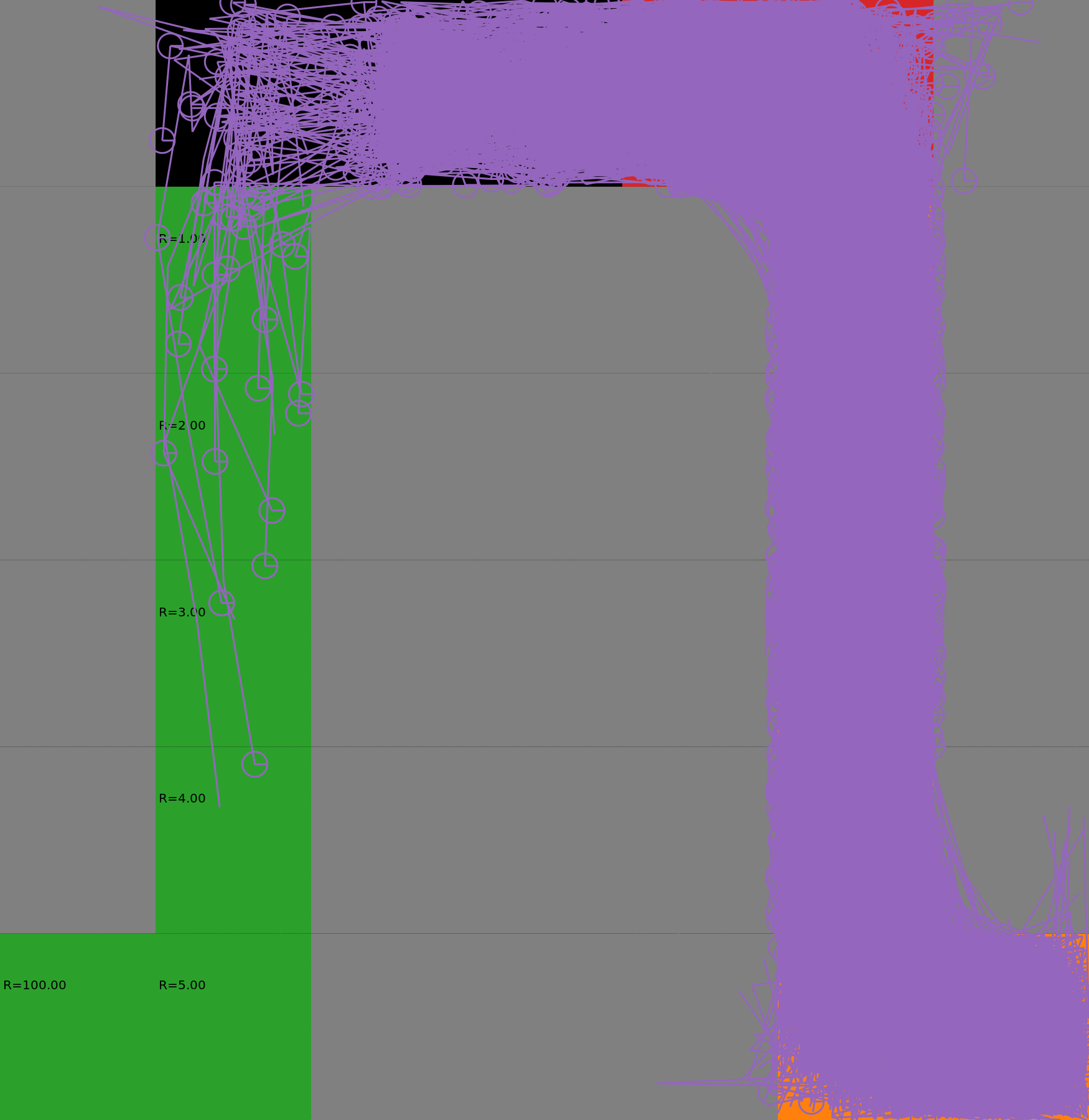
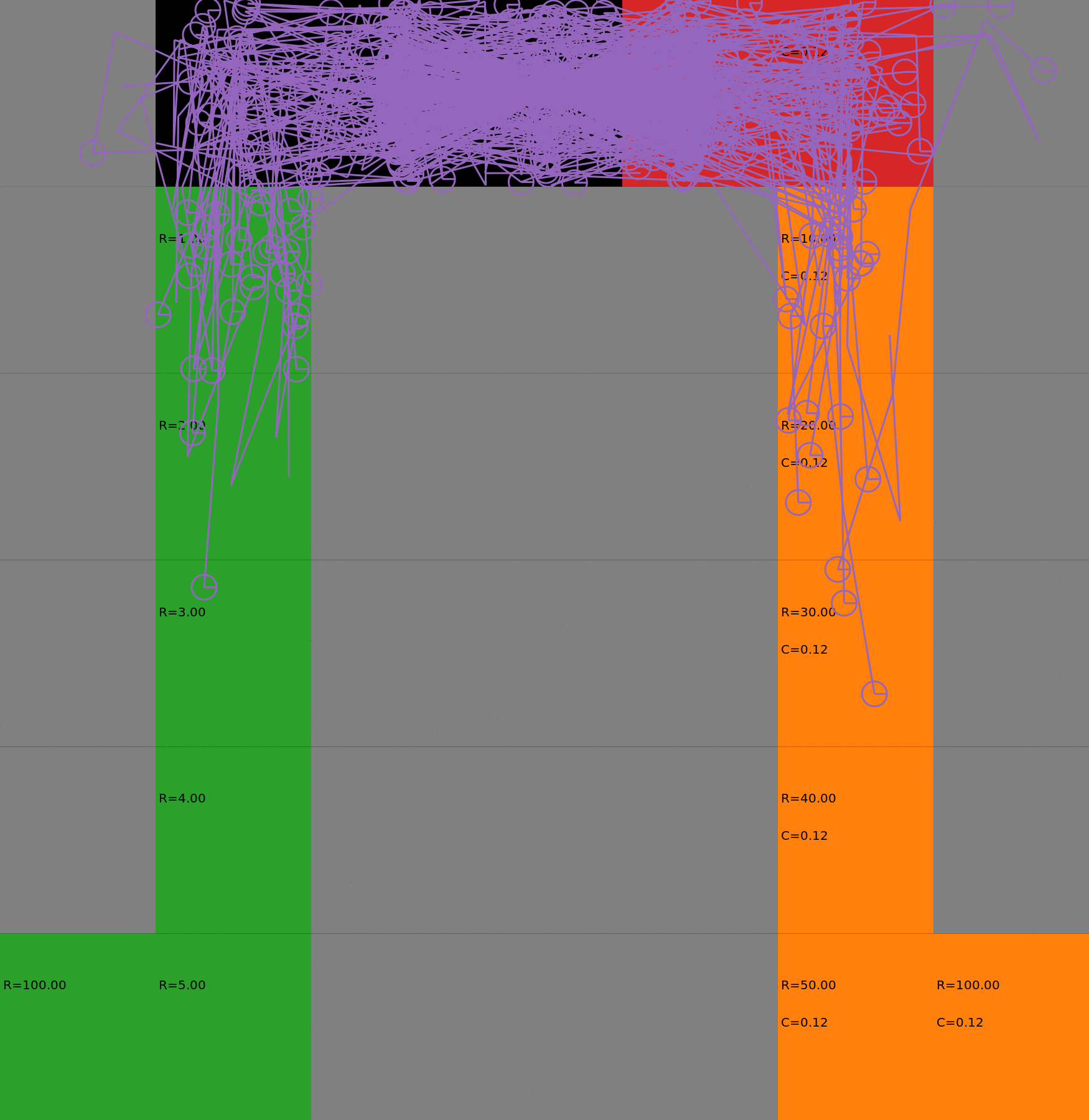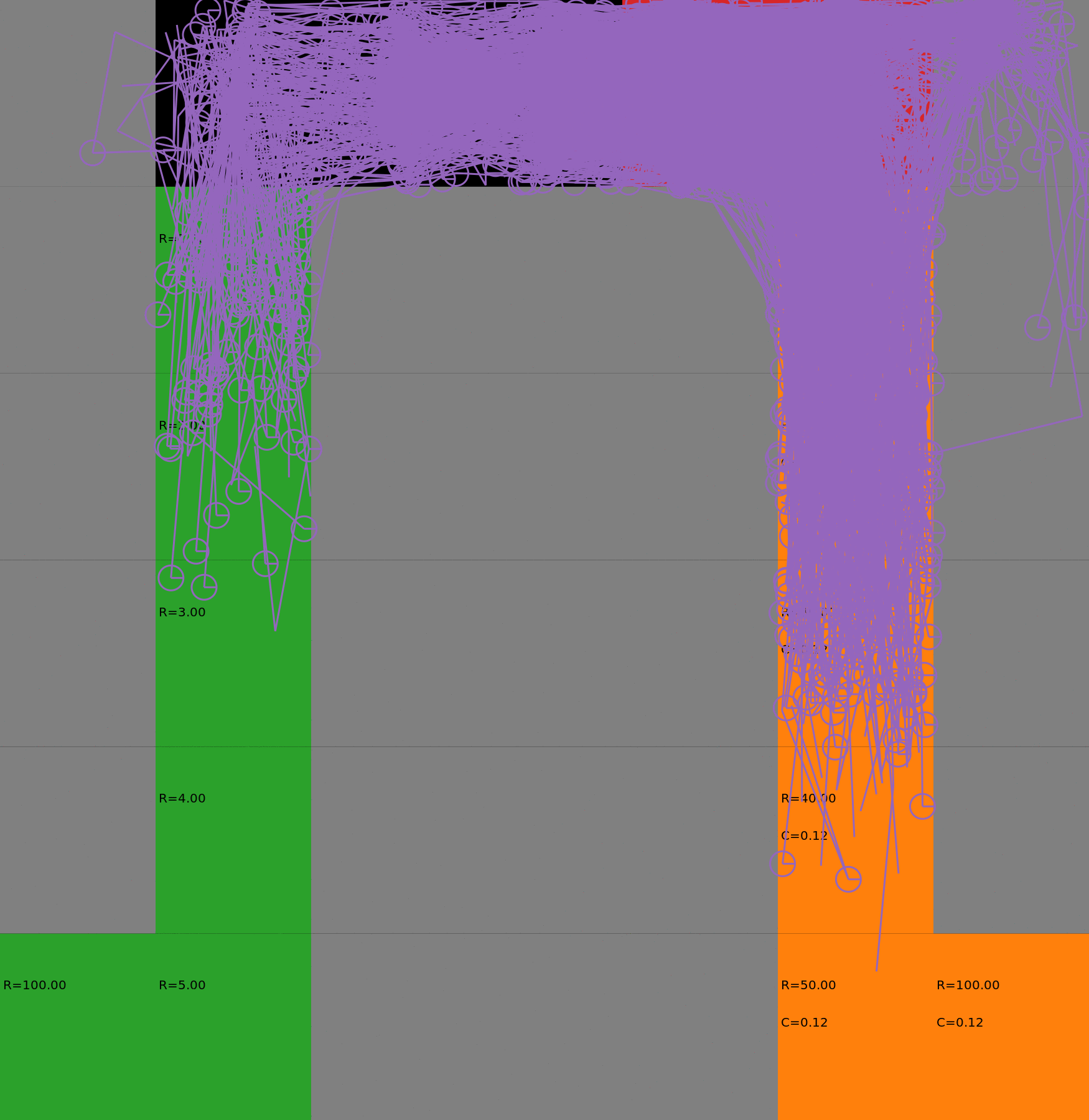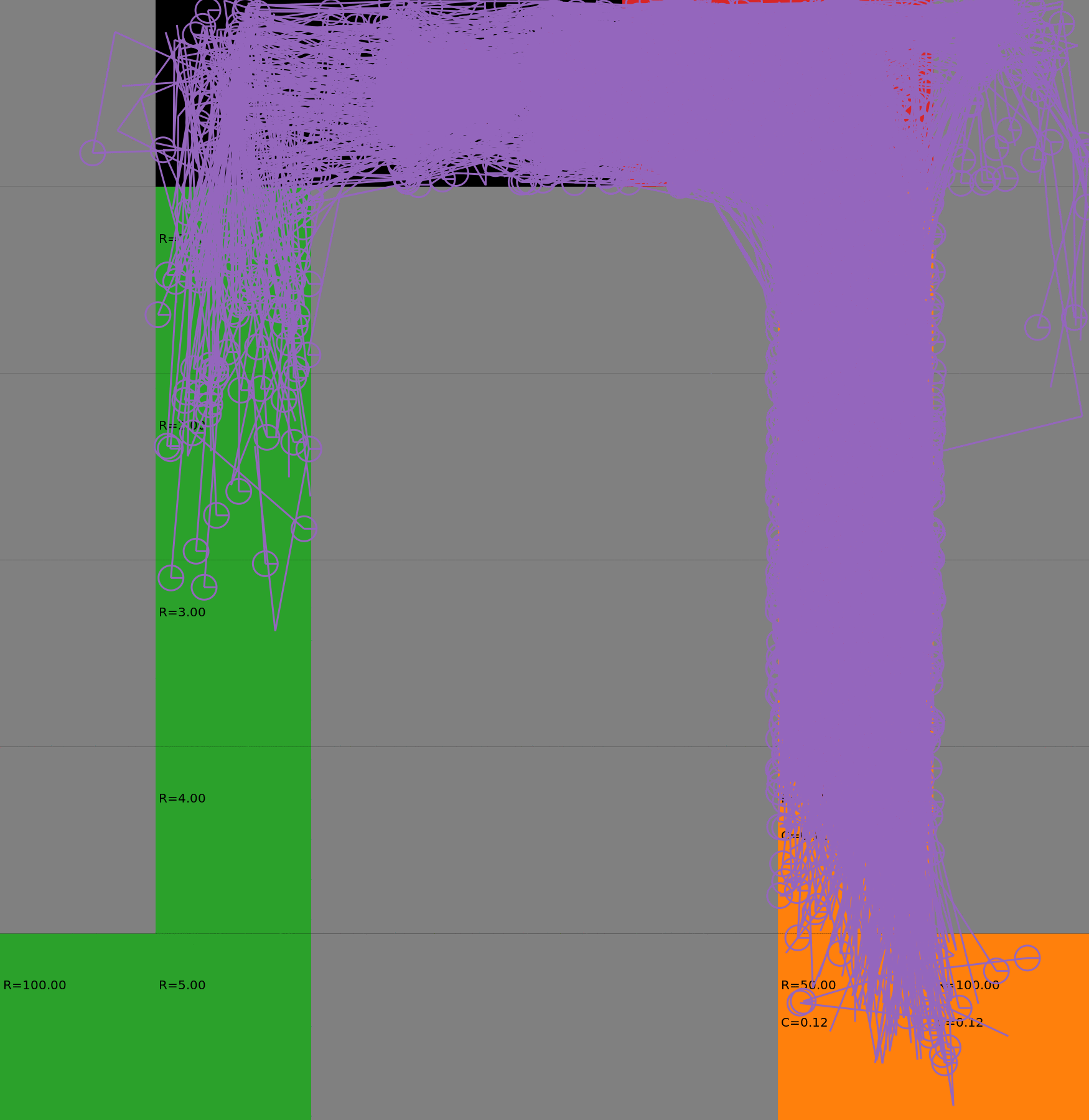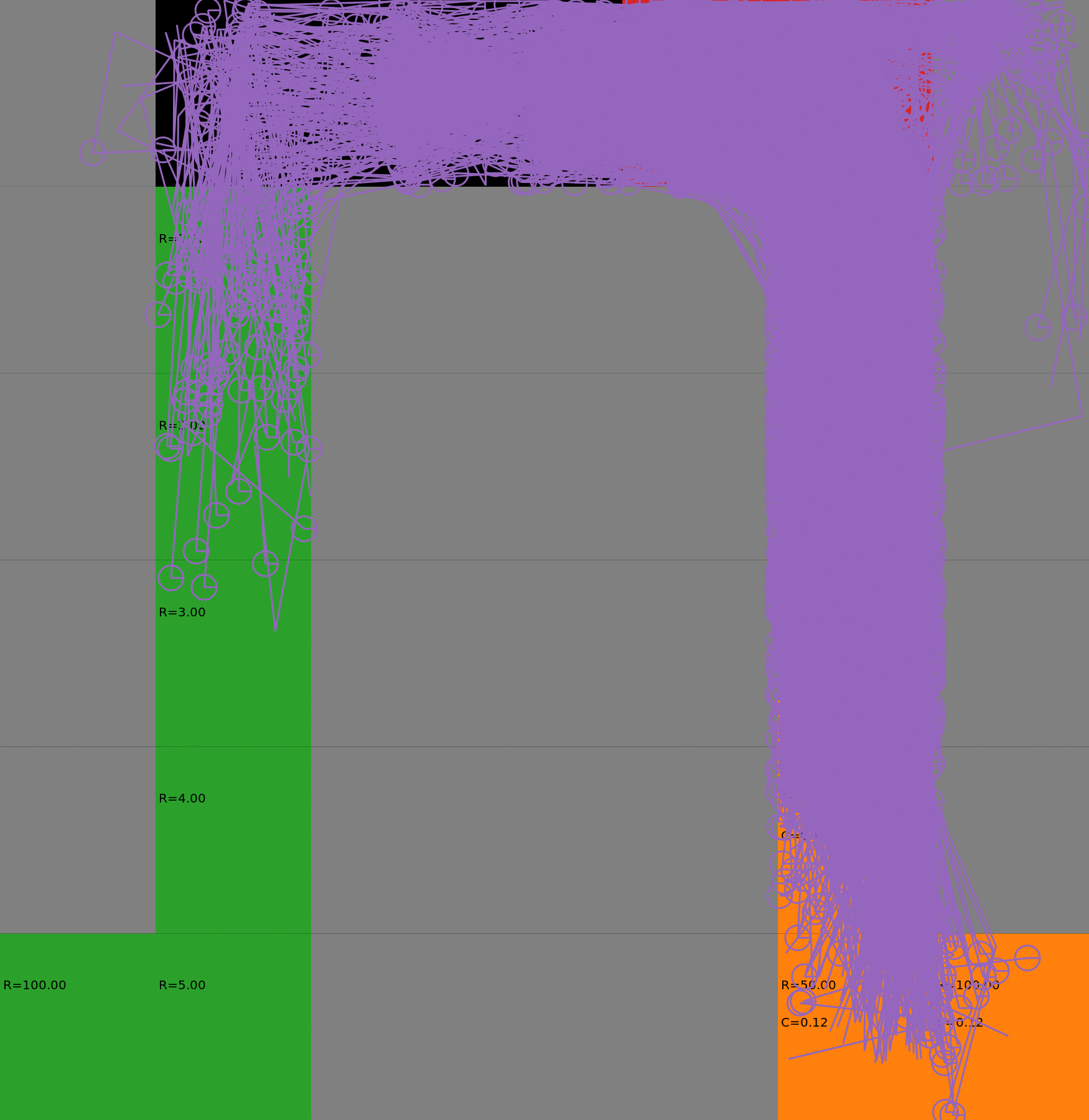
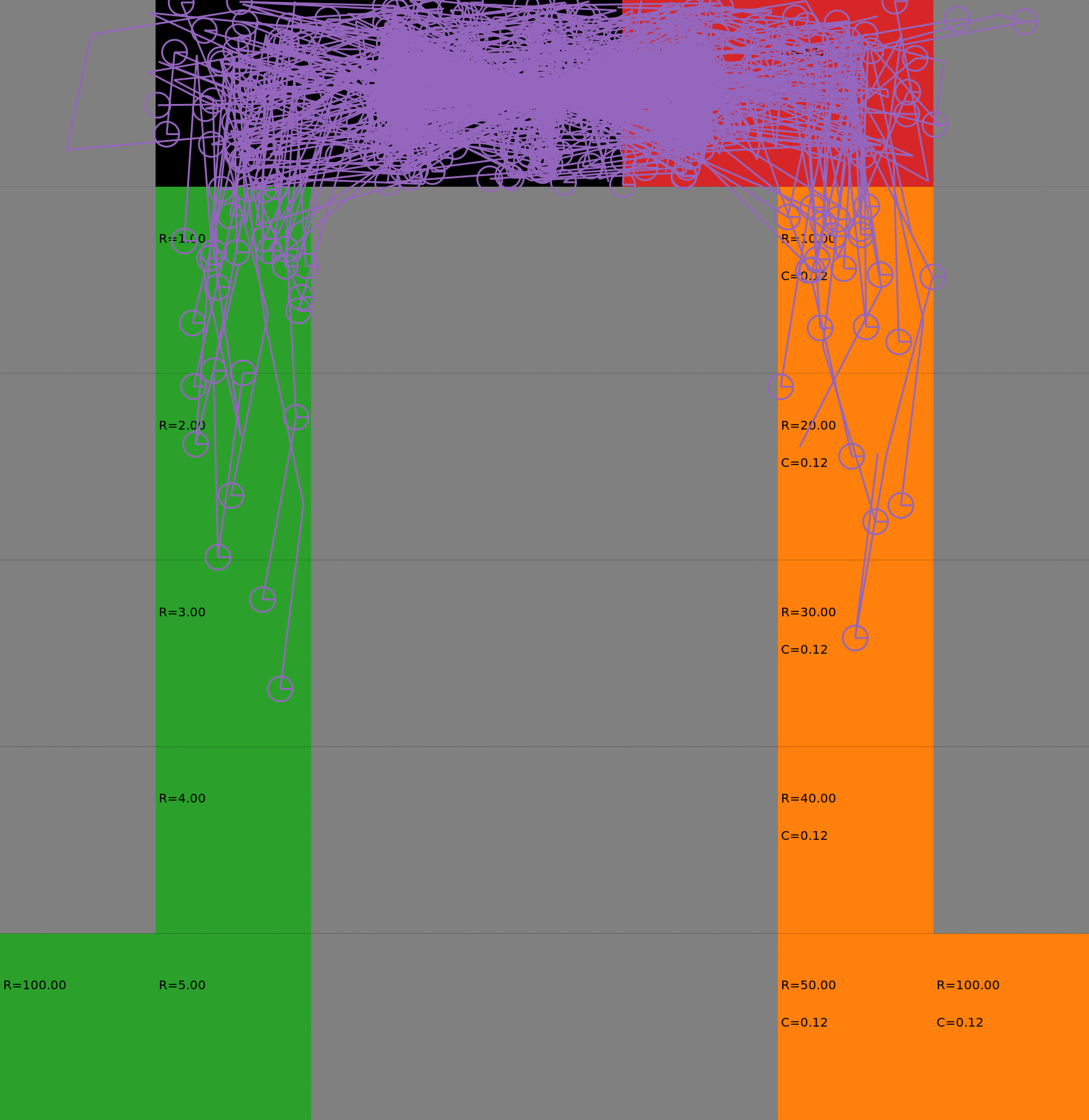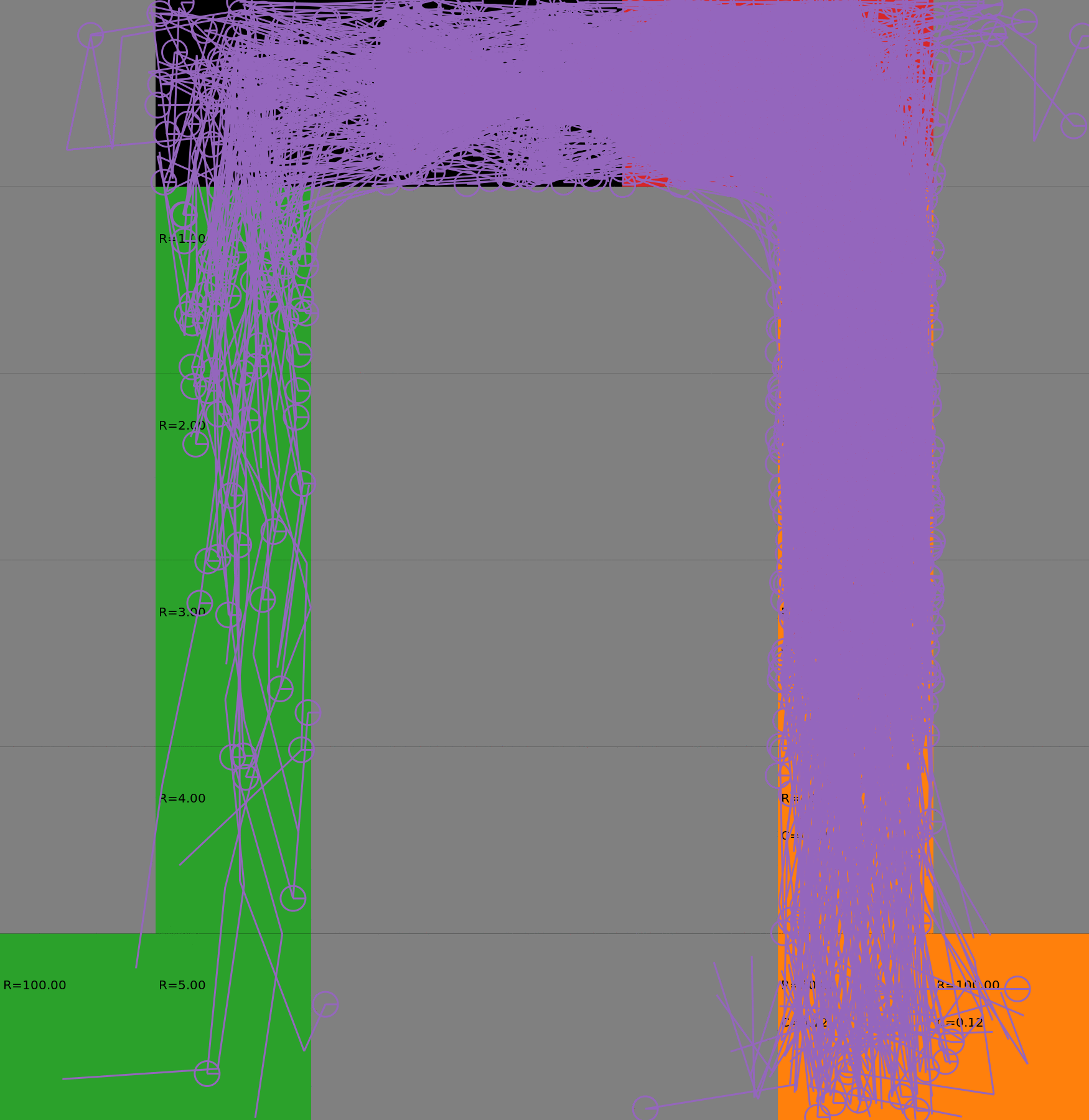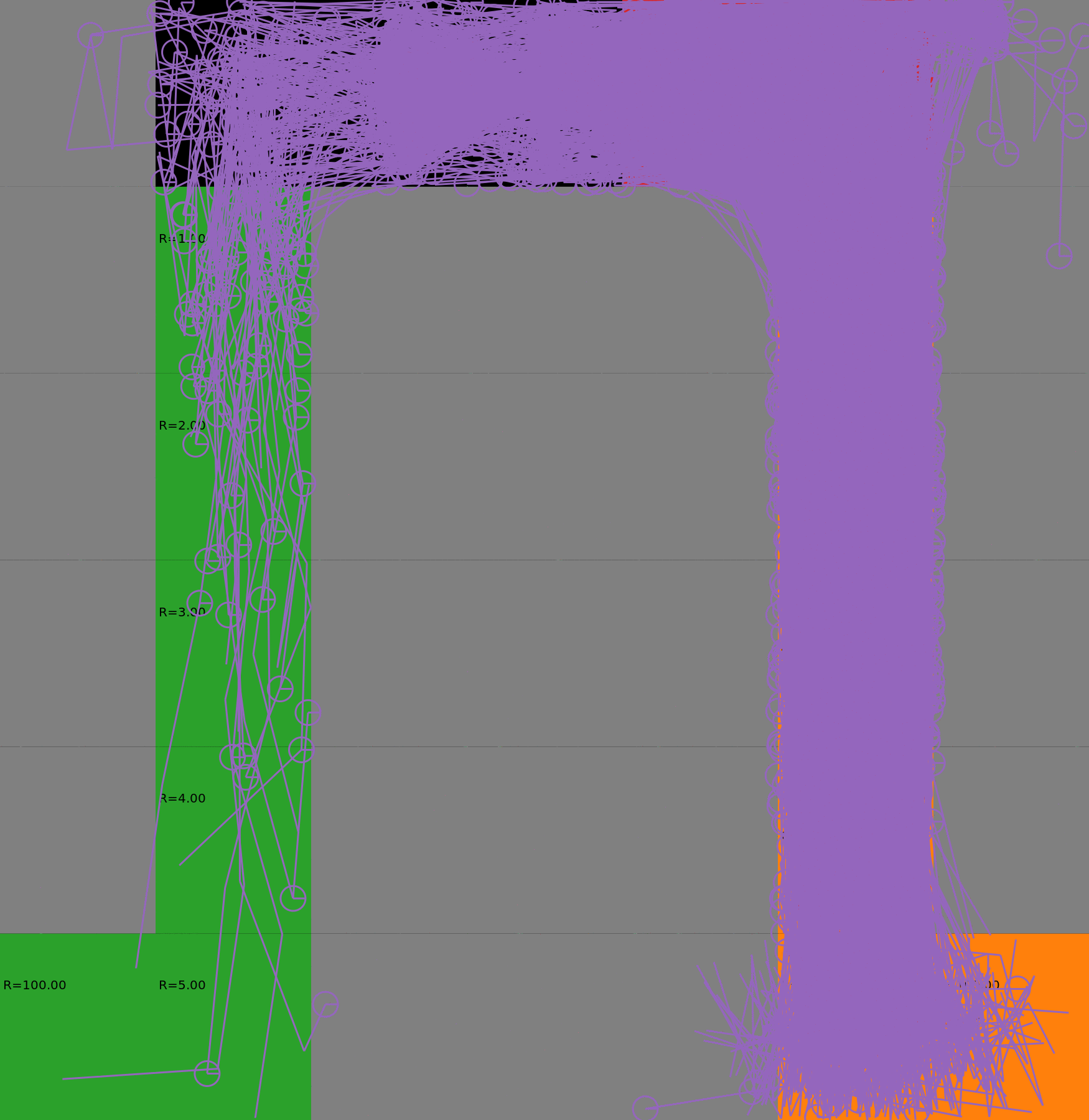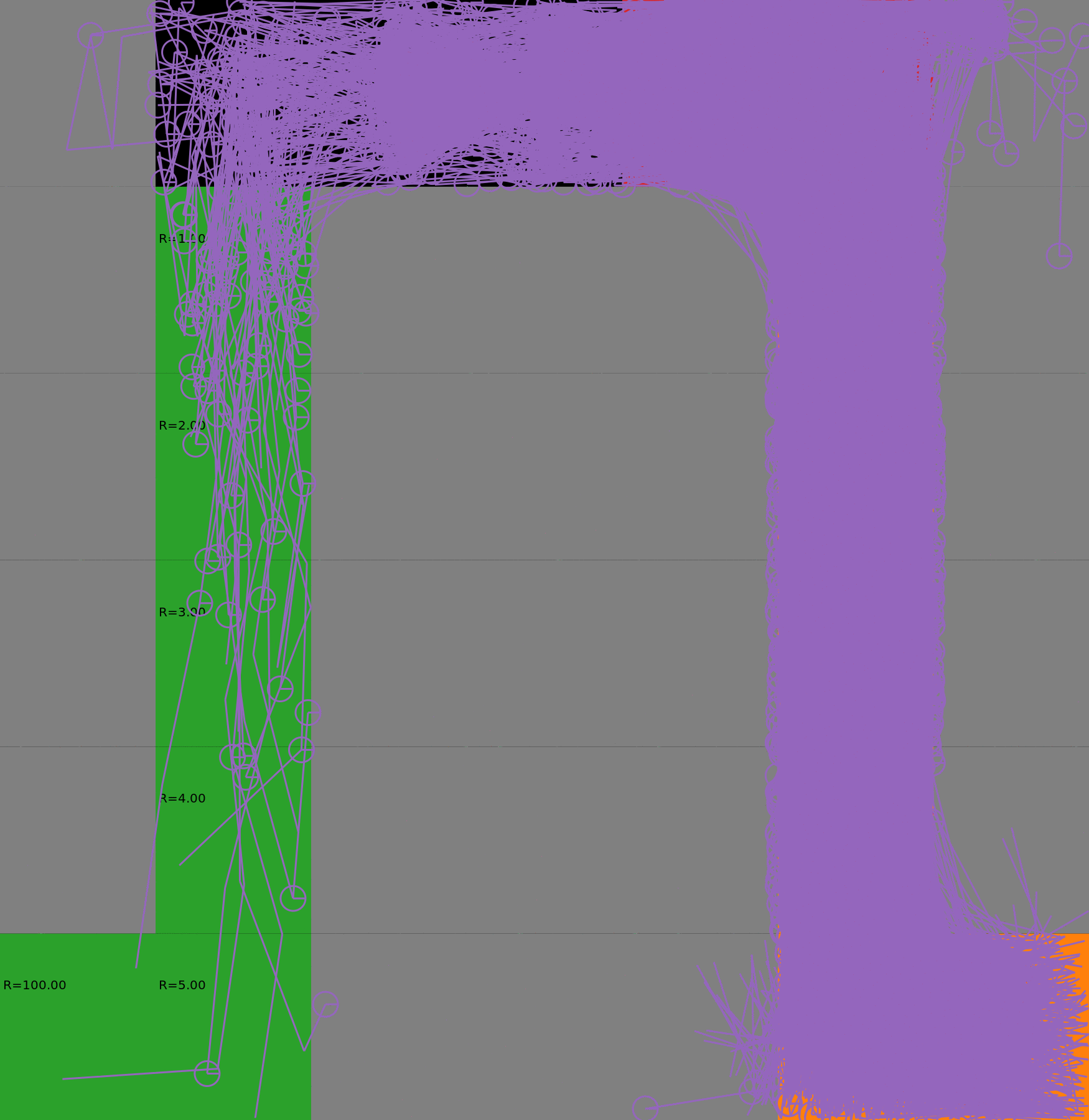
Risk-sensitive strategy
Optimal Budgeted Policies learnt with a risk-sensitive exploration
We display the evolution in the budgeted policy behavior with respect to the budget. The policies have been learnt with a risk-sensitive exploration. When the budget is low, the agent takes the safest path on the left. When the budget increases, it gradually switches to the other lane, earning higher rewards but also costs. This gradual process could not be achieved with a deterministic policy as it would chose either one path or the other. Each animation corresponds to a different seed.
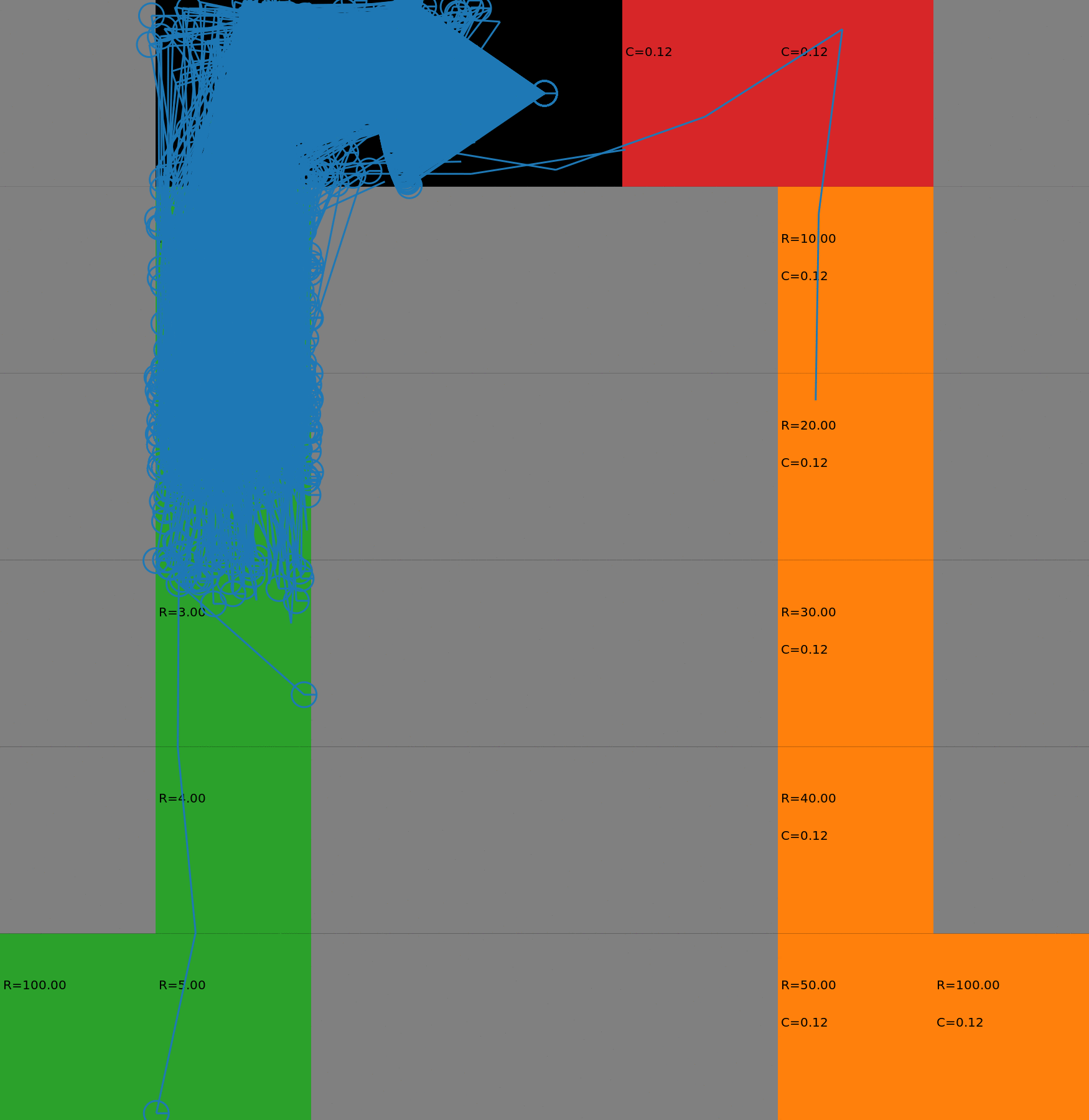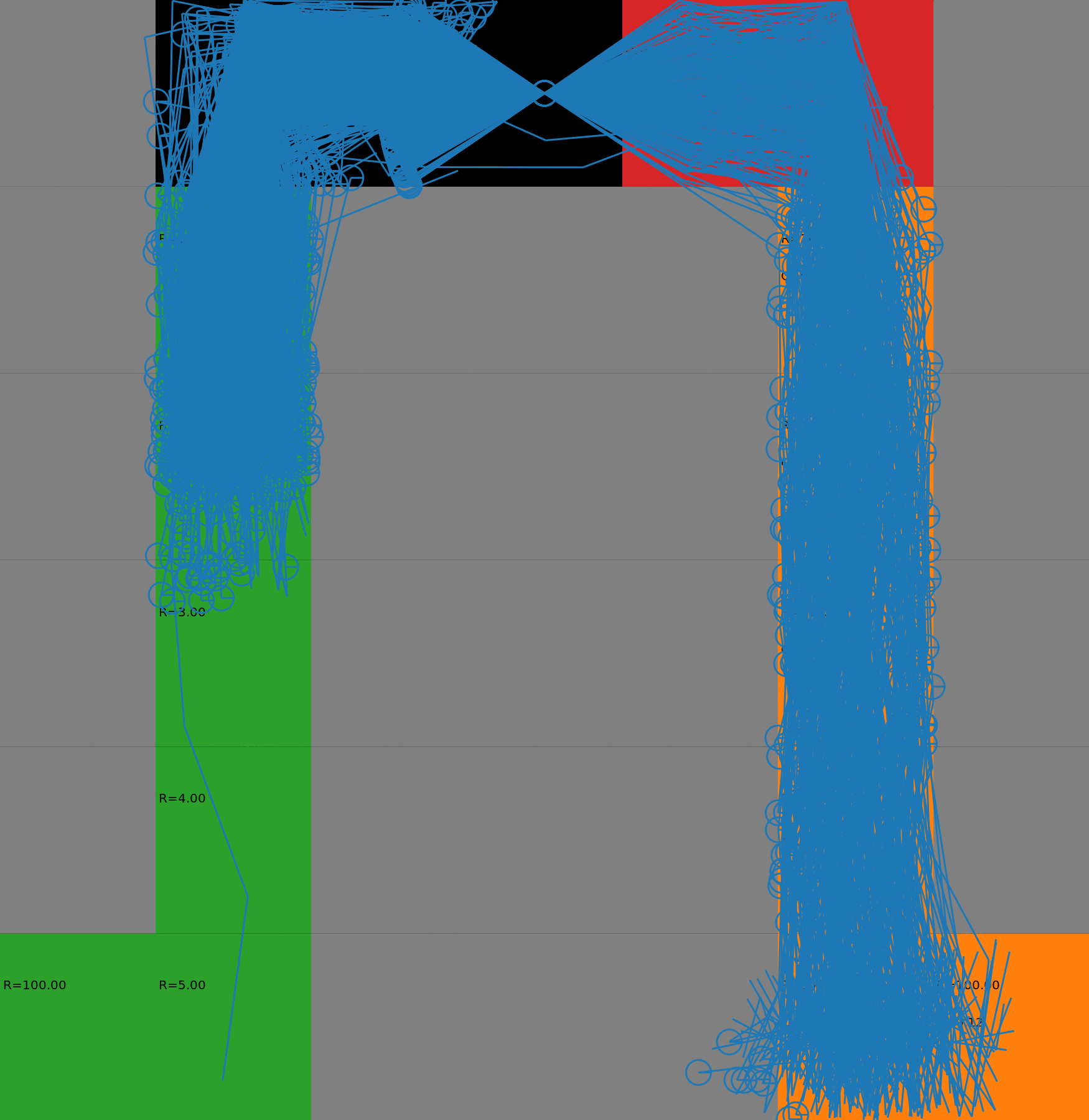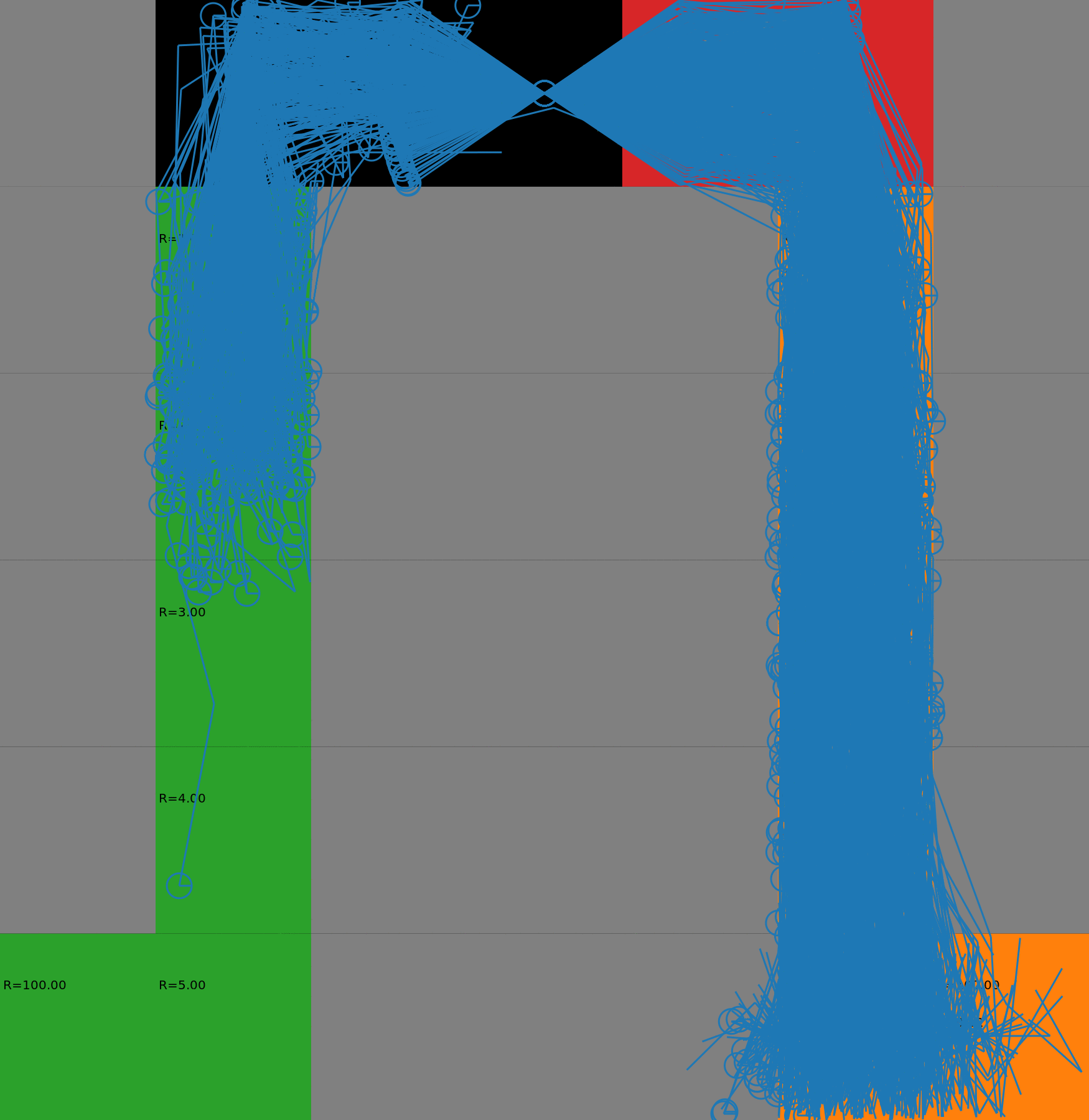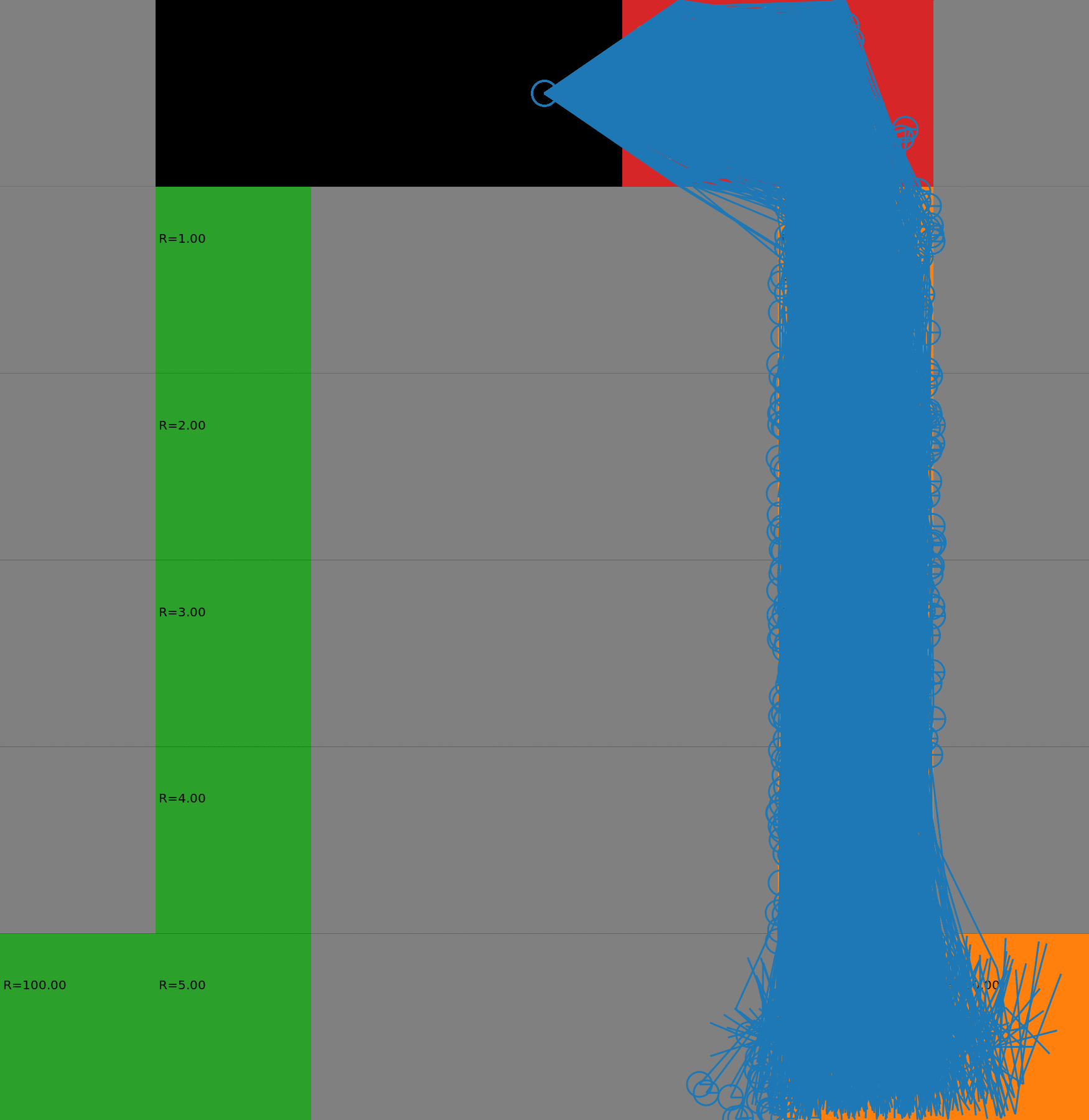


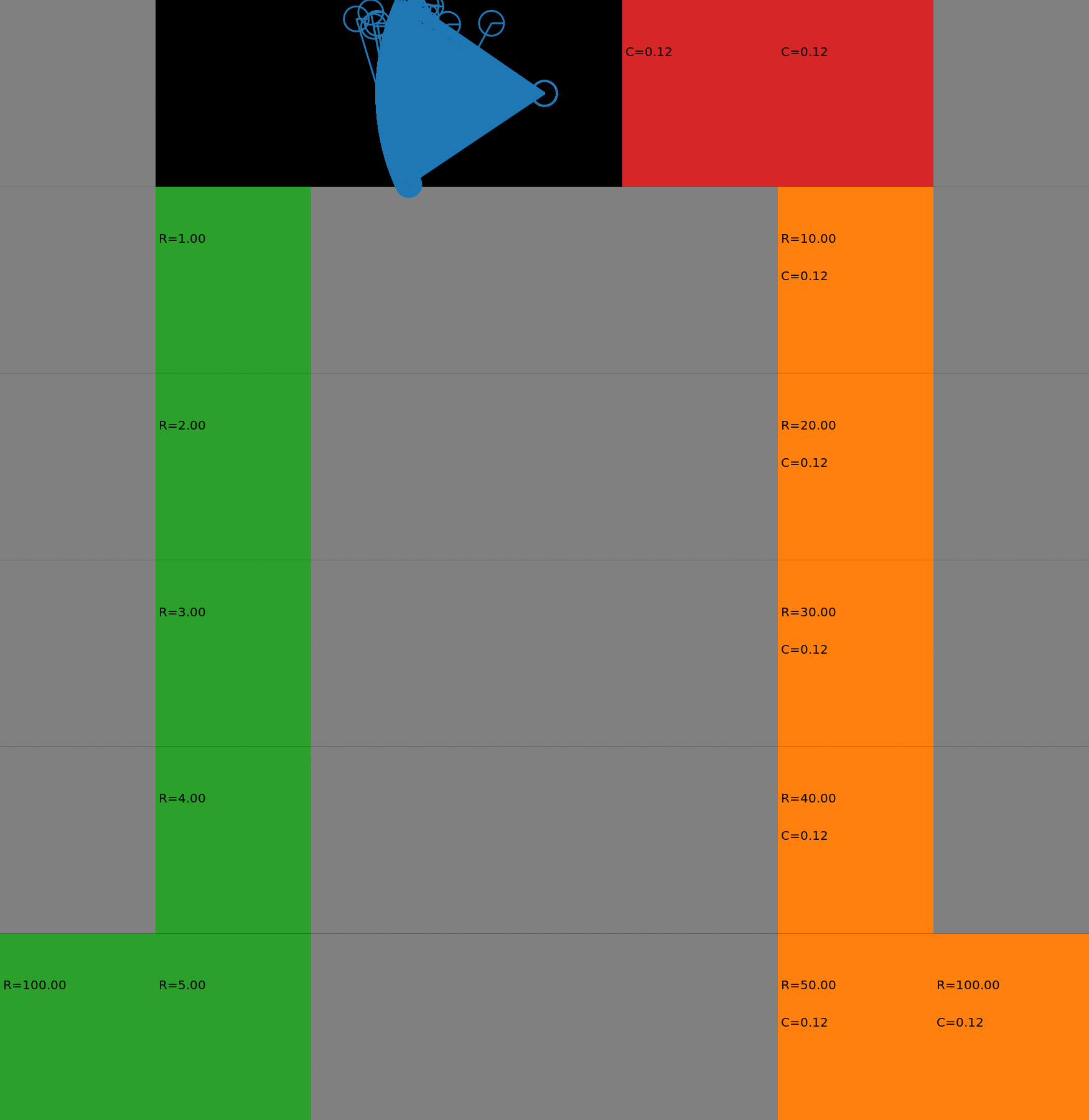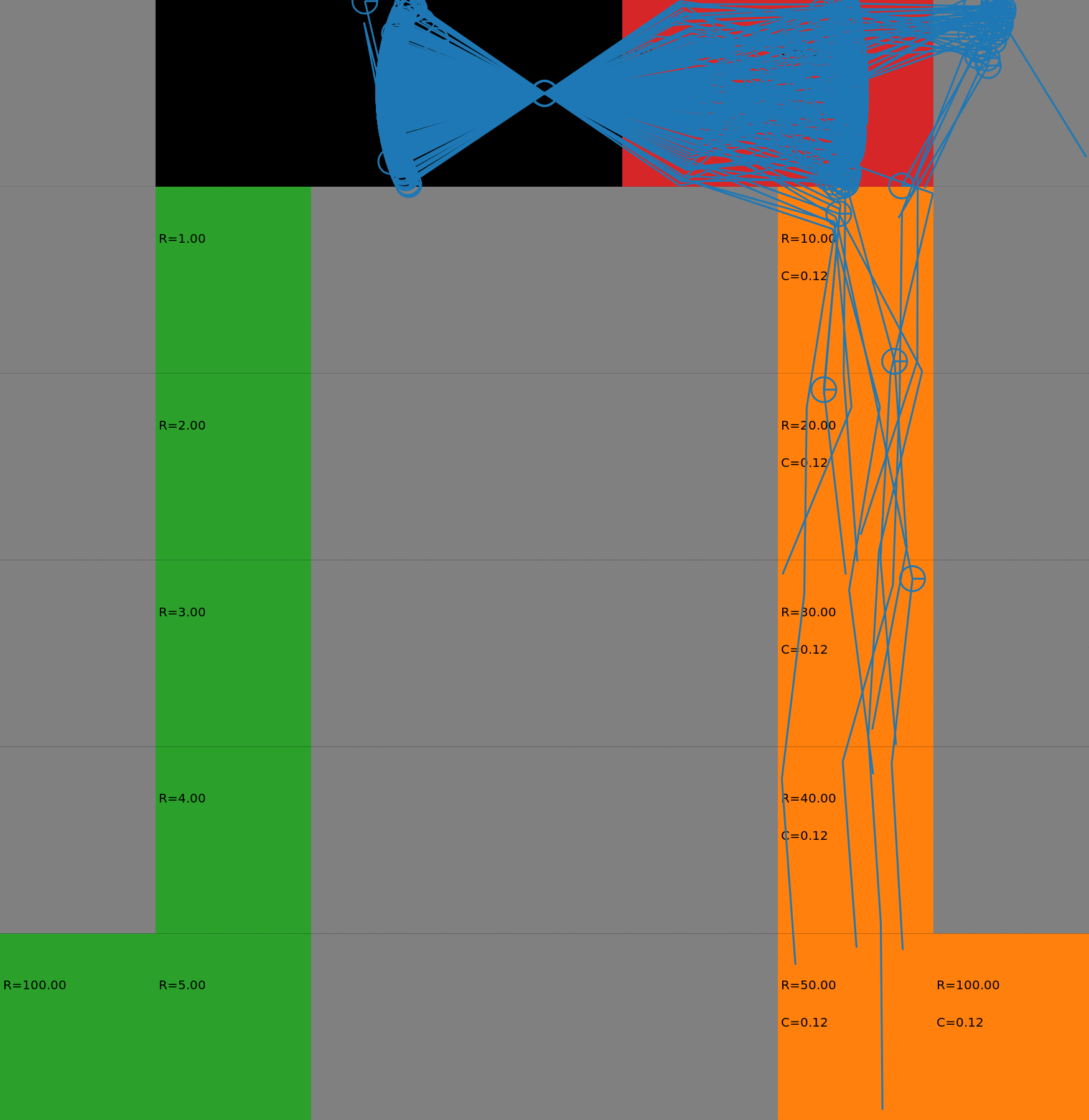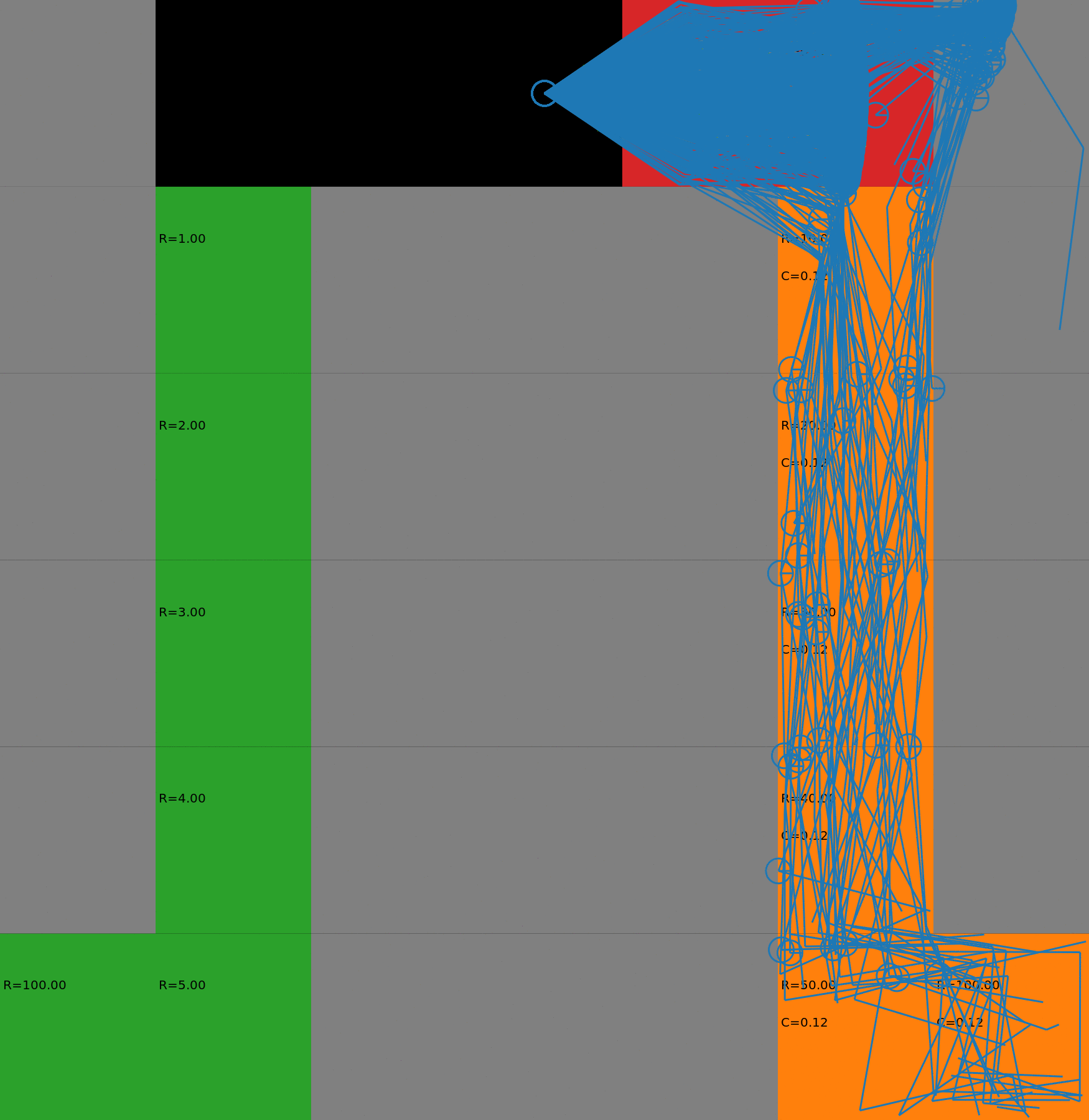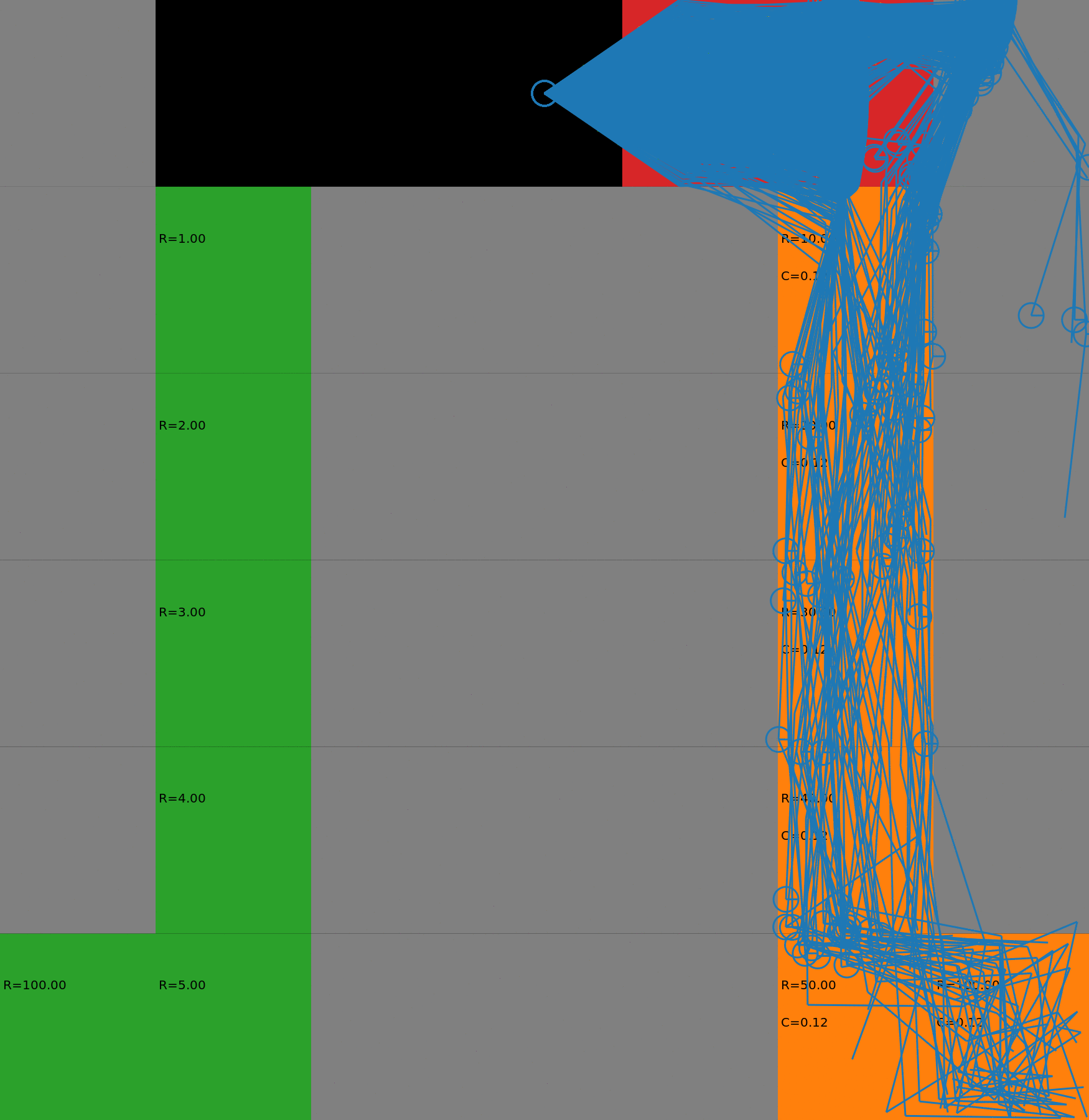
How to reproduce
First install the following conventional libraries for python3: pycairo, numpy, scipy and pytorch. Install the highway-env environment. Then, use one of these methods:
Method 1 (for highway-env: repository eleurent)
Install requirements:
- The agents: eleurent@rl-agents
Run the training:
cd <path-to-rl-agents>/scripts/
python experiments.py evaluate scripts/configs/TwoWayEnv/env.json \
scripts/configs/TwoWayEnv/agents/BFTQAgent/baseline.json \
--train --episodes=1000
Method 2 (for slot-filling, highway-env,and corridors: repository ncarrara)
- Clone ncarrara@budgeted-rl
- Change python path to the path of this repository
export PYTHONPATH="budgeted-rl/ncarrara" - Navigate to budgeted-rl folder
cd budgeted-rl/ncarrara/budgeted-rl - Run main script using any config file. Choose the range of seeds you want to test on:
python main/egreedy/main-egreedy.py config/slot-filling.json 0 6 python main/egreedy/main-egreedy.py config/corridors.json 0 4 python main/egreedy/main-egreedy.py config/highway-easy.json 0 10
Environment parameters
Corridors
| Parameter | Description | Value |
|---|---|---|
| - | Size of the environment | 7 x 6 |
| - | Standard deviation of the Gaussian noise applied to actions | (0.25, 0.25) |
| H | Episode duration | 9 |
Slot-Filling
| Parameter | Description | Value |
|---|---|---|
| ser | Sentence Error Rate | 0.6 |
| Gaussian mean for misunderstanding | -0.25 | |
| Gaussian mean for understanding | 0.25 | |
| Gaussian standard deviation | 0.6 | |
| Probability of hang-up | 0.25 | |
| H | Episode duration | 10 |
| - | Number of slots | 3 |
Highway-Env
| Parameter | Description | Value |
|---|---|---|
| Number of vehicles | 2 - 6 | |
| Standard deviation of vehicles initial positions | 100 m | |
| Standard deviation of vehicles initial velocities | 3 m/s | |
| H | Episode duration | 15 s |
Algorithms parameters
Corridors
| Parameters | BFTQ(risk-averse) | BFTQ(greedy) |
|---|---|---|
| architecture | 256x128x64 | 256x128x6 |
| regularisation | 0.001 | 0.001 |
| activation | relu | relu |
| size beta encoder | 3 | 3 |
| initialisation | xavier | xavier |
| loss function | L2 | L2 |
| optimizer | adam | adam |
| learning rate | 0.001 | 0.001 |
| epoch (NN) | 1000 | 5000 |
| normalize reward | true | true |
| epoch (FTQ) | 12 | 12 |
| 0:0.01:1 | - | |
| beta for duplication | 0:0.1:1 | 0:0.1:1 |
| (1,1) | (1,1) | |
| 5000 | 5000 | |
| 10 | 10 | |
| 4 | 4 | |
| 1000 | 1000 | |
| decay epsilon scheduling | 0.001 | 0.001 |
Slot-Filling
| Parameters | BFTQ | FTQ |
|---|---|---|
| architecture | 256x128x64 | 128x64x32 |
| regularisation | 0.0005 | 0.0005 |
| activation | relu | relu |
| size beta encoder | 50 | - |
| initialisation | xavier | xavier |
| loss function | L2 | L2 |
| optimizer | adam | adam |
| learning rate | 0.001 | 0.001 |
| epoch (NN) | 5000 | 5000 |
| normalize reward | true | true |
| epoch (FTQ) | 11 | 11 |
| 0:0.01:1 | - | |
| beta for duplication | - | - |
| (1,1) | (1,1) | |
| 5000 | 5000 | |
| 10 | 10 | |
| 6 | 6 | |
| 1000 | 1000 | |
| decay epsilon scheduling | 0.001 | 0.001 |
Highway-Env
| Parameters | BFTQ | FTQ |
|---|---|---|
| architecture | 256x128x64 | 128x64x32 |
| regularisation | 0.0005 | 0 |
| activation | relu | relu |
| size beta encoder | 50 | - |
| initialisation | xavier | xavier |
| loss function | L2 | L2 |
| optimizer | adam | adam |
| learning rate | 0.001 | 0.01 |
| epoch (NN) | 5000 | 400 |
| normalize reward | true | true |
| epoch (FTQ) | 15 | 15 |
| 0:0.01:1 | - | |
| beta for duplication | - | - |
| (0.9, 0.9) | (0.9, 0.9) | |
| 10000 | 10000 | |
| 10 | 10 | |
| 10 | 10 | |
| 150 | 150 | |
| decay epsilon scheduling | 0.0003 | 0.0003 |
Acknowledgements
This work has been supported by CPER Nord-Pas de Calais/FEDER DATA Advanced data science and technologies 2015-2020, the French Ministry of Higher Education and Research, INRIA, and the French Agence Nationale de la Recherche (ANR). We thank Guillaume Gautier, Fabrice Clerot, and Xuedong Shang for the helpful discussions and valuable insights.
